hi Kannitverstan,
sowas ähnliches hab ich auch rausbekommen, nur auflösen geht nicht bei mir. bin da über math42 dran gegangen, aber die sind nun weg vom Fenster, weil verkauft. und auf die Bezahl App ( 10 €/mtl) hab ich kein Bock. . .
glaub mir, diese Aufgabe macht mich fertig (lächel)
Wie weiter?
bin soweit gegangen und habe über Excel den Winkel Alpha interpoliert, um ein Näherungswert zu bekommen . nur - reine Mathematik geht anders. . . .
Magst du das mal ein bisschen breiter ausführen, bitte?
Mich würde die Lösung auch interessieren.
Gruß
F.
Das obere Dreieck (ABD) hat ja den selben Winkel alpha wie das untere Dreieck.
Eine Spiegelung an der Seite x (Streck BD) führt dazu, dass die Seite m auf der Seite z zu liegen kommt.
Erkenntnis: Die Höhe des unteren Dreiecks BCD beträgt 3.
(Bild folgt!)
Hier hast du Foto.
Mir war nämlich zuerst nicht klar, warum beim oberen Dreieck die Seitenlänge „3“ überhaupt relevant sein sollte. Dann erkannte ich, dass damit die Höhe bestimmt wird.
Vielen Dank, das habe ich soweit gut verstanden, steh aber trotzdem auf dem Schlauch …
Da der Fußpunkt der Höhe nicht der Punkt E sein wird, und mir deshalb die angegebene Länge von BE nicht hilft, finde ich um unteren Dreieck (außer Rechtwinkligkeit) keine weitere Angabe, mit der ich über die Kenntnis der Höhe dann weiter kommen könnte.
Darf ich dich nochmal bitten 
Gruß
F.
Die Erkenntnis, dass AD die Höhe des Dreiecks BCD ist, ist in der Tat noch nicht mal die halbe Miete, auch wenn man zur Flächenberechnung von ECD dann ‚nur‘ noch z benötigt. Das ‚Umklappen‘ verdeutlicht übrigens zusätzlich, dass m gleich dem längeren Hypotenusenabschnitt von BCD ist. Die Ähnlichkeit von BCD mit ABD wurde schon genannt. Was hier noch nicht angesprochen wurde ist, dass n eine Winkelhalbierende ist. Somit ist z / 5 = y / x und daher z = 5 * tan ά. Der Tangens eines Winkels entspricht dem Quotient aus Sinus und Cosinus, also ist tan ά = sin ά / cos ά wobei hier sin ά = 3 / x und cos ά = x / ((5 + z) ist. Somit ist tan ά = 3 * (5 + z) / x² = (15 + 3z) / x².
Außerdem ist tan ά = 5 / z, somit ist (15 + 3z) / x² = 5 / z - ergibt über
z(15 + 3z) = 5x² ausmultipliziert 3z² + 15z = x². Wenn man jetzt noch wüsste, wie groß x ist …
Schaun mer mal den Euklid’schen Höhensatz an: m (5 + z - m) = 9, ausmultipliziert 5m + zm – m² = 9 und aus der Ähnlichkeit der Dreiecke ergibt sich x / (5 + z) = m / x bzw. x² / (5 + z) = m. Eingesetzt in den Höhensatz:
5(x² / (5 + z)) + z(x² / (5 + z)) – (x² / (5 + z))² = 9
5x²(1 / (5+z)) + zx²(1 / (5+z)) – x²(1 / (5+z)) = 9
5x² + zx² – x² = 45 + 9z
x² (5 + z - 1) = 45 + 9z
x² = (45 + 9z) / (4 + z)
Damit haben wir zwei Gleichungen mit denselben beiden Unbekannten, jeweils nach x² aufgelöst, was zu Folgendem führt:
3z² + 15z = (45 + 9z) / (4 + z)
12z² + 60z + 3z³ + 15z² = 45 + 9z
3z³ + 27z² + 51z = 45
z³ + 9z² + 17z - 15 = 0
Eine kubische Gleichung für z. So - und jetzt habe ich den Spass an der Beschäftigungstherapie verloren. Habe auch keine Lust mehr nachzuprüfen, ob ich da irgendwo einen Denk - oder Rechenfehler gemacht habe. Einen schönen Abend noch.
Ralf
Hi Tychiades,
die Notwendigkeit, den Winkelhalbierenden-Satz einzubeziehen, sah ich auch. Ich hab ihn allerdings anders verwendet. Siehe unten.
soweit richtig. Aber dann rechnest du mit einem Fehler weiter:
denn tan α = z / 5, und somit 3 * (5 + z) / x² = z / 5.
In der weiteren Überlegung mit dem Höhensatz:
5x²(1 / (5+z)) + zx²(1 / (5+z)) – x²(1 / (5+z)) = 9
5x² + zx² – x² = 45 + 9z
muß es heißen:
5x²(1 / (5+z)) + zx²(1 / (5+z)) – x²(1 / (5+z)²) = 9
5x² + zx² – x²/(5+z) = 45 + 9z
usw.
Das führt insgesamt aber ebenfalls zu einer (allerdings komplizierteren) kubischen Gleichung in z.
Gruß
Metapher
Einen anderen Ansatz als @Tychiades → oben versuchte ich über die direkte Flächenberechnung (aus der z eliminiert wird):
Die Teilfläche [BED] des Dreiecks BCD ergibt sich ja mit der Höhe h = AD = 3 und der Grundlinie BE = 5 zu
[BED] = 3 * 5 / 2
Die gesuchte Fläche [ECD] ist dann die Differenz der Flächen [BCD] - [BED]. Es wäre also [BCD] zu berechnen.
Für [BCD] gilt
(1) [BCD] = xy /2
und
(2) [BCD] = (5+z) * 3 / 2
Ferner gilt:
(3) x² + y² = (5+z)²
Aus (1) und (2) folgt:
(4) xy = 3 * (5+z)
Aus dem Winkelhalbierenden-Satz folgt:
y / x = z / BE = z / 5
z = 5 * y / x
z in (3):
(3a) x² + y² = (5 + 5 * y / x)² = 25 * (1 + y / x)²
z in (4)
(4a) xy = 3 * (5 + 5 * y / x) = 15 * (1 + y / x)
Ich bin aber nicht sicher, ob die Überlegung sinnvoll ist. Denn
(5) x² + y² = x²y² / 9 = ergibt siich ja schon aus (3) und (4), und es wäre eine weitere Gleichung für x und y zu finden.
Gruß
Metapher
Danke und 
@Tychiades und @Metapher quasi für die Bestätigung meines Verdachts, dass es für das Problem des UP keine „einfache“ Lösung gibt.
Gruß
F.
mit der höhe 3 hast du mir neue Impulse gegeben. aaaaaber: die Höhe i3 ist nicht notwendigerweise die Mittelsenkrechte. Wäre es die Mittelsenkrechte, könnte man flott durchrechnen und käme auf ein Ergebnis.
ist aber nicht.
damit ist eine Variable weg, es bleiben aber noch die variablen Alpha, x und z.
mal sehen, wer da schlaue Antworten hat.
lg
ralf
Höhe 3 ( ohne i)
Mein (recht deutlicher) Verdacht ist, dass es überhaupt keine Lösung gibt. Gewissermaßen eine Scherzaufgabe (ich hatte es ja schon als „Beschäftigungstherapie“ bezeichnet). Gar nicht ungeschickt gemacht; etliche mögliche Ansätze, die aber alle ins Leere laufen. Neben den genannten (Höhensatz, Ähnlichkeitssätze, Winkelhalbierendensatz usw.) gilt das übrigens auch für den Sinussatz (sin α / n = sin 45° / 5 = sin (135° - α) / x sowie sin α / 3 = sin 90° / x = sin (90° - α) / x). @ralf_g_nther hält sich ja auch bedeckt hinsichtlich der Quelle der Aufgabe - aus dem schulischen Mathematikunterricht kommt das wohl kaum …
Gruß,
Ralf (der andere)
Wenn Du das, nachdem Du angeblich mit der Aufgabe „schon mehrere Wochen am rummachen“ warst, nicht selbst gemerkt hast, hast Du Dir das falsche Hobby ausgesucht.
Natürlich nicht - und niemand hier hat solch einen Unsinn behauptet.
Die Antworten, die Du bislang gekriegt hast, waren jedenfalls allemal schlauer als alles, was Du selbst beigesteuert hast. Selbst die triviale von @X_Strom …
Hallo Tychiades
upps, da habe ich ja richtig was losgetreten. (wofür steht die Abk. UP??? unlösbares Problem??)
über die Aufgabe hab ich mir auch so meine Gedanken gemacht wie du mit Höhensatz, Ähnlichkeitssätze, Winkelhalbierendensatz usw. und kam nicht weiter.
Der Dreh- und Angelpunkt bei der Aufgabe ist winkel Alpha. hast du Alpha, hast du die Lösung.
so einfach.
Dann bin ich hingegangen und habe Alpha über Excel durchlaufen lassen (interpoliert) und bin auf einen Winkel von „ungefähr“ 26,565 Grad gekommen.
nur mit diesem Winkel gehen alle Angaben auf - ungefähr natürlich
Damit gibt es eine Lösung, nur den mathematischen Lösungsweg kenne ich nicht. und den Rest der community auch nicht.
Tychiades, geh doch einfach hin und rechen die Aufgabe stumpf durch mit Alpha = 20 bzw Alpha = 30 Grad. Die Sache funzt nicht.
Das macht die kirre.
im Anhang habe das „umgeklappte“ Dreieck gestellt. Sieht einfacher aus, hilft aber auch nicht weiter. . .
Hallo!
Ich bin nicht wirklich auf nen grünen Zweig gekommen, habe das aber zumindest mal nachkonstruiert. Fakt ist: Es gibt eine Lösung, und sie lautet 3,75.
Meine Konstruktion sieht so aus:
Bleibt evtl. die Frage, ob das obere Dreieck denn nun auch wirklich noch dazu passt. Aber… das Dreieck BDV ist die gespiegelte Version davon, und wegen der Parallelen ist α=β. Das passt also.
Ich habe das ganze mit Geogebra konstruiert, und dann den Winkel und die Fläche messen lassen. Der Winkel ist krumm, aber die Fläche hat nen recht glatten Wert. Das ist natürlich nicht der Lösungsweg, aber zum Verifizieren taugt das allemal.
Da die Versuche, Lösungsgleichungen über die Flächeninhalte zu finden, zu Gleichungssystemen führte, die nicht unahöngig sind, hab ich es noch einmal über die Ähnlichkeiten der Dreiecke gemacht. was dann zur Lösung führt:
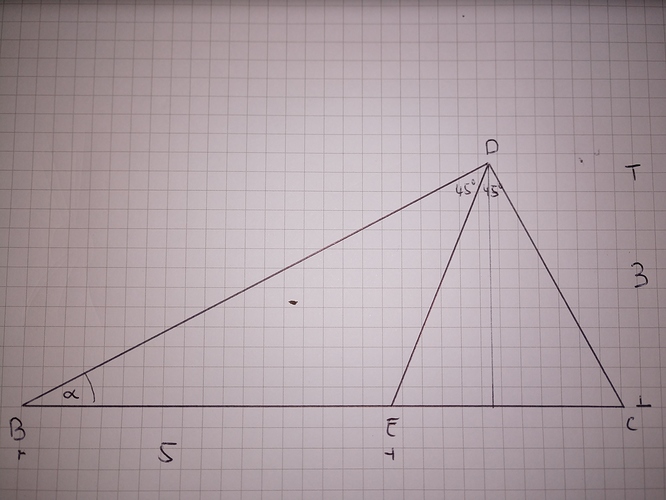
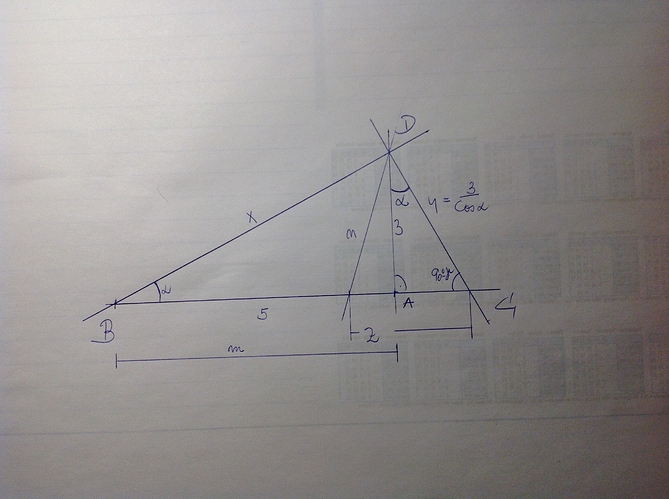
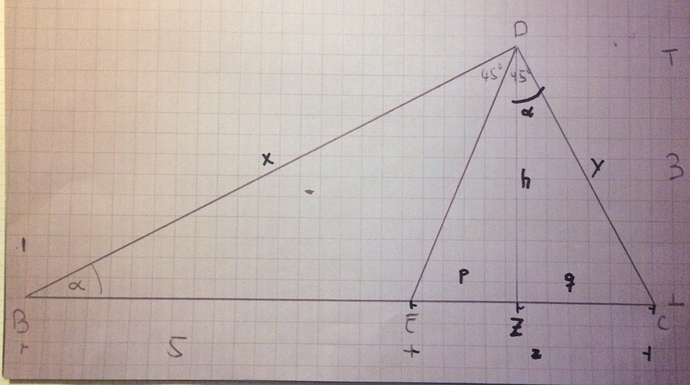
Zur Bezeichnung der benutzten Strecken hab ich die Ziichnung von @X_Strom vervollständigt:
Folgende Dreiecke sind ähnlich:
BDC
BZD
DZC
es gilt:
x / y = (5 + p) / h = h / q
Mit h = 3 folgt
(1) x / y = (5 + p) / 3 = 3 / q
Daraus:
(2) q * (5+p) = 9
Der Winkelhalbierenden-Satz ergibt:
(3) x / y = 5 / (p + q)
(1) und (3) ⇒
5 / (p + q) = 3 / q
⇒
(4) q = 3p / 2
(2) und (4) ⇒
3p / 2 * (5 + p) = 9
p² + 5p - 6 = 0
mit der Lösungmenge p = {-6 | 1}, wobei p = 1 hier relevant ist.
Mit (2) ⇒ q = 3 / 2
Also
z = q + p = 2,5
und somit die Lösung
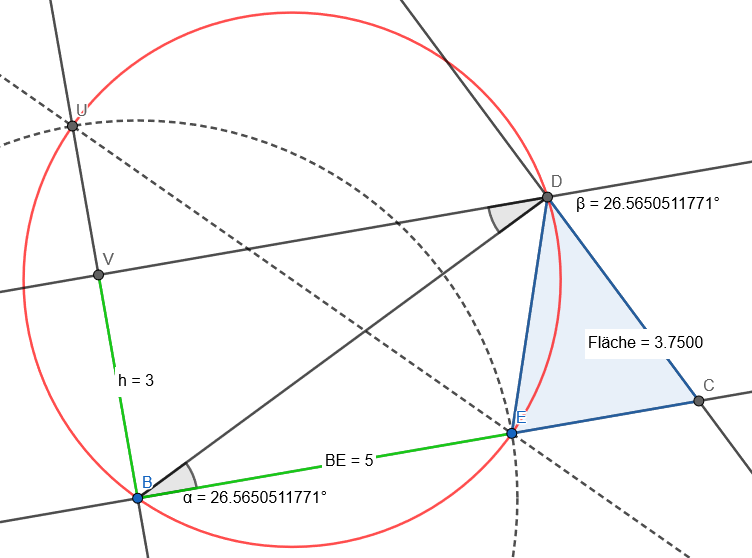
[ECD] = h * z / 2 = 3,75
Zur Probe:
Es gilt ja [ECD] = [BDC] - [BED]
[BDC] = (5 + z) * h / 2 = (5 + 2,5) * 3 / 2 = 11,25
[BED] = 5 * h / 2 = 7,5
[BDC] - [BED] = 3,75 = [ECD] q.e.d.
Gruß
Metapher
addendum
es folgt btw. tan α = 0,5 und somit α = 26.566°
Irgendwie hab Ich den Punkt links unten anfangs mit A bezeichnet. Ich meine natürlich die ganze Zeit B!
Aber ist doch schön, daß sich die Werte mit den berechneten von @Metapher decken!
Kein Prob, denn es war leicht zu erkennen. Du hast aber letztlich die Aufgabenstellung als solche lediglich mit einer anderen Methode rekonstruiert - allerdings mit einer sehr interessanten Idee: Thaleskreis über E und U (= Umkreis EBU) und dann dazu den Sehnensatz.
Daraus ist erkennbar, daß das Dreieck BED aus den zwei Größen BE und h eindeutig bestimmt ist, wenn die dritte Bedingung hinzukommt, daß D auf dem Umkreis von Dreieck BEU liegend soll (das ist identisch mit der Angabe des Winkels 45° bei D). Damit ist dann auch BCD bestimmt und folglich auch ECD. Das war aber eh aus der Aufgabenstellung klar. Deshalb musste es eine Lösung geben.
Aber daß der Flächeninhalt [ECD] und auch α mit der Lösung übereinstimmt, ist nicht verwunderlich. Du hast ja lediglich die Konstruktion wiederholt. Dein Programm hat aber die Lösung nicht aus der geometrischen Konstrultion direkt entnommen, sondern mutmaßlich aus den Koordinaten der Punkte berechnet.
Gruß
Metapher
Korrekt.
Und natürlich ist gefordert, die Fläche aus der gegebenen geometrie zu berechnen, aber wenn man numerisch schonmal die Werte zum Vergleich hat, ist das ja auch nicht verkehrt.
Übrigens, „mein“ Programm ist Geogebra, mittlerweile eine Webanwendung: www.geogebra.org . Damit kann man sowas gut konstruieren, und es sieht auch noch wunderschön aus.
