Das erscheint mir zu ungenau.
Ist Dein Haus rechtwinklig? Nimm den Zeitpunkt, an dem die Sonne die Vorderseite bescheint, die beiden Flanken aber im Schatten liegen. Gleiches machst Du mit der Flanke. Was kommt heraus?
Och, stetig ist er (mathematisch gesehen)…
Nochmal ein ganz anderes Beispiel:
Ein Bogenschütze schießt einen Pfeil gradeaus, dreht sich um 15°, und schießt den nächsten Pfeil, und so weiter. Die Flugbahnen der Pfeile unterscheiden sich also alle um exakt 15°.
Nun steht da eine lange, grade Mauer, die von den Pfeilen getroffen wird. Der Abstand der in der Mauer steckenden Pfeile ist nun aber nicht konstant, sondern wird nach außen hin immer größer. Die beobachtete Größe (Abstand der Pfeile in der Mauer) ergibt sich aus einem geometrischen Zusammenhang, bei dem allerdings die konstanten 15° verloren gehen.
Mit deinem Sonnenlicht ist es genauso. Die Sonne bewegt sich entlang ihrer Bahn zwar um 15° weiter schräg über den Himmel, aber Azimut und Elevation ändern sich aus geometrischen Gründen nicht um konstante Werte.
Noch ein Extrembeispiel: Du begibst dich an einen Ort bei 22,5° nördlicher Breite. Dort geht morgen die Sonne exakt im Osten auf, steigt senkrecht hoch in den Himmel, bis sie mittags exakt über die steht, und sinkt dann senkrecht nach Osten herab, bis sie exakt im Osten untergeht. Die Elevation ändert sich hier um 15° pro Stunde. Aber der Azimut bleibt bis Mittags bei 90° (Osten), um sich dann sprunghaft auf 270° (Westen) zu ändern. Da ist überhaupt nichts mit Änderung, bis auf diesen einen Sprung.
Sphärische Geometrie ist leider etwas schwierig zu erklären und zu verstehen.
Das nenn’ ich mal eine tolle Versinnbildlichung!![]()
![]() .
.
Btw. , wegen Breitengrad entlangfliegen: ist auch nur auf dem Globus (eigentlich über dem Globus) „Luftlinie“.
Auf Karten verzerrt bogenförmig.
Gruss, Kudo
sweber, weiß nicht, ob Chrizz es jetzt versteht, ich aber leider noch nicht. Würde ich aber gerne.
Dein Beispiel mit der Mauer und den Pfeilen verstehe ich gut. Auch das Beispiel von der Sonne, die über den Zenit läuft.
Aber was ist nun mit Chrizz Haus… angenommen, er hat wirklich ziemlich exakt richtig gemessen (hört sich so an, Bodenfliesen).
Die Sonne beschreibt doch jeden Tag einen Kreis von 360 Grad um sein Haus (naja, in Wirklichkeit dreht sich die Erde um die Sonne und ganz exakte Kreise sind das nie, aber das ist vermutlich nicht entscheidend).
Im Sommer ist der größere Teil der Sonnenbahn über, der Rest unter dem Horizont.
Wenn die Sonne tagsüber scheinbar „zu schnell“ ist, müsste sie nachts gewissermaßen langsamer sein…Warum? Woran liegt das?
Und ist das im Winter anders?
Wie du siehst, kann ich mir das noch nicht vorstellen!
Karl
Hi!
Das ist recht schwer noch weiter zu erklären. Vielleicht nochmal so:
Das Haus im Süden, bei dem die Sonne durch den Zenit läuft, ist der Azimut morgens konstant bei 90° (ost), und die Elevation steigt mit 15° pro Stunde, bis die Sonne im Zenit steht. In einem Wimpernschlag ändert sich der Azimut dann auf exakt 270° (West), und die Elevation fällt um 15° pro Stunde. Das heißt, die rote Kurve oben ist zweigeteilt - ein konstanten Stück bei 90° bis mittags, und dann ein zweites konstantes Stück bei 270°. Und die Elevation geht schnurgrade bis 90°, um dann ganz plötzlich ab Mittag wieder schnurgrade runter auf 0° zu gehen.
Betrachte noch ein anderes Extrembeispiel. An Nordpol steht die Sonne grade den ganzen Tag in einer konstanten Elevation von 67,5° über den Horizont, was in der Grafik eine konstante, waagerechte blaue Kurve ergibt. Dafür ändert sich hier der Azimut tatsächlich um 15°/Stunde, die rote Kurve ist dann eine exakte, steigende Grade.
Wir liegen nun genau dazwischen. Also bei der roten Kurve zwischen zwei konstanten Einzelstücken und der perfekten Grade, was die geschwungene Form ergibt. Und die Elevation ist auf dem Weg vom perfekten „Dreieck“ zur perfekten konstanten Funktion.
Ursächlich für das ganze ist, dass sich das Haus und das Grundstück nicht nur einfach mit um die Erdachse dreht, sondern die Erdachse zusätzlich noch um 22° gekippt ist. Beides zusammen ergibt eine scheinbare Bewegung, bei der die 15° nicht mehr zu sehen sind.
Und wie eingangs gesagt, hier wird ausschließlich der Azimut betrachtet..
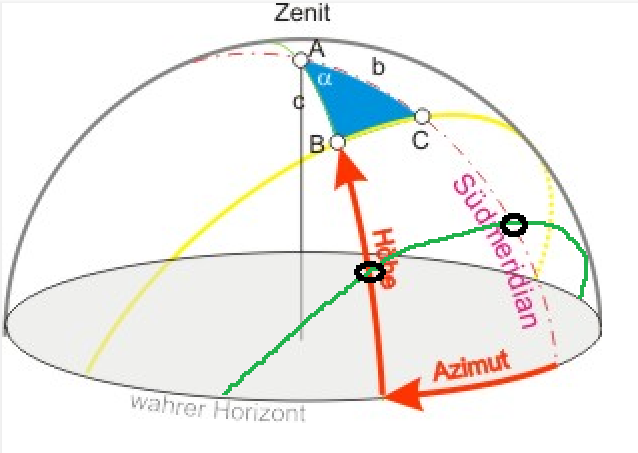
Ich hab mal übel in einem Bild rumgekrakelt:
Gelb die Bahn im Sommer, grün die Bahn im Winter. Die Geschwindigkeit der Sonne auf ihrer Bahn ist konstant, aber um Mittags den Winkel alpha zu überstreichen, ist der Weg im Winter länger.
Auf der gegenüberliegenden Seite (= nachts) ist es genau umgekehrt. Da ist Weg von B nach C auf der gelben Bahn länger und auf der grünen Bahn kürzer.
Die scheinbare Geschwindigkeit der Sonne auf ihrer Bahn ist immer gleich, nur das Azimut ändert sich im Verlauf von 24 Stunden mit unterschiedlicher Rate.
Das ganze ist außerdem vom Breitengrad des Beobachters abhängig - am Nord- und Südpol verläuft die Sonnenbahn parallel zum Horizont, da ist die Azimutänderung pro Zeit über 24 Stunden konstant.
Zwischen den Wendekreisen schwankt der Wert über 24 Stunden am stärksten, bis hin dazu dass es zweimal im Jahr einen Sprung um 180° gibt (wenn die Sonne durch den Zenit wandert)
Danke Sweber und KHK, ich glaube, ich habe es verstanden. Werde mir die sache nochmal in Ruhe selber durchdenken! Eure Beispiele und Grafiken sind jedenfalls hilfreich!
Karl
Ich habe diese Antwort jetzt als Lösung markiert. Ich habe einige Seiten gefunden, auf denen man diese Berechnung für den eigenen Standort machen kann. Ich habe etwas dazugelernt. Und mit einer Wette hätte ich viel Geld verloren. Allein: ich verstehe immer noch nicht, wie das sein kann. ![]()
Ich werde die hier präsentierten Beispiele aber noch eingehend studieren und nachvollziehen.
Vielen Dank an alle und Grüße aus Belgien.
Irgendeine Spreizung würde ich ja auch akzeptieren, aber einen während der Tageslänge hin und her variierenden Azimuthverlauf muß ich erst verdauen. Mit Zigarre und Whisky. ![]()
Dieses Thema wurde automatisch 30 Tage nach der letzten Antwort geschlossen. Es sind keine neuen Nachrichten mehr erlaubt.