Hallo,
wie lautet eine allgemein gültige Formel für diese Rechnung:
B = Basiswert
B^1 + B^2 + B^3 … + B^n
Ich bin auf das hier gekommen. Das passt auch, aber das geht sicher auch einfacher.
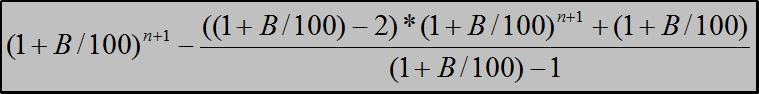
Danke und Gruß
Martin
Hallo,
wie lautet eine allgemein gültige Formel für diese Rechnung:
B = Basiswert
B^1 + B^2 + B^3 … + B^n
Ich bin auf das hier gekommen. Das passt auch, aber das geht sicher auch einfacher.
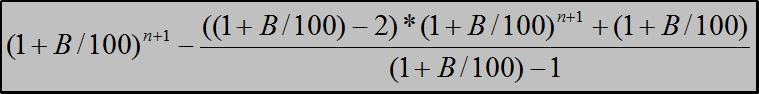
Danke und Gruß
Martin
Hallo,
ist mir zu umständlich, alles aufzuschreiben, deshalb hier der Link mit der Herleitung: Geometrische Reihe – Wikipedia
Danke, aber das ist ja noch komplizierter.
Meine Formel konnte ich noch ein wenig vereinfachen
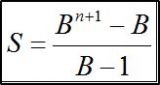
Das muss ich jetzt noch nach n und B auflösen.
n hab ich geschafft:
![]()
Bei der Auflösung nach B hänge ich noch ein wenig. Weiter als bis hier komme ich nicht:
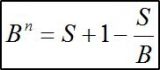
Kann mir jemand die letzten Schritte zeigen?
Danke und Gruß
Martin
Verstehe ich nicht, nach B^n umstellen, wäre ja wohl eine einfache Addition. S_n = B^1 + … + B^n und damit B^n = S_n - S_{n-1}.
Aber jetzt steh ich doch vor dem Problem, dass ich S(n-1) nicht habe und auch nicht berechnen kann, denn dazu bräuchte ich B ![]() .
.
Oder steh ich auf dem Schlauch?
Danke
Martin
Ich verstehe ehrlich gesagt nicht, was Du eigentlich willst. Du hast eingangs gefragt, wie lautet die Formel für B^1 + … + B^n, mit B ein fester Basiswert. Da sagt Dir jeder Mathematiker, das ist die Partialsumme der geometrische Reihe (minus B^0). In der ganzen Gleichung stehen drei Parameter, B und n und die Partialsumme (s). Kennst Du je zwei Parameter, dann kennst Du auch den dritten.
Also, was meinst Du mit „allgemein gültige Formel“, was kennst Du, was sucht Du?
Was ich will.
Was ich habe.
Formeln für 1. und 2.
Was ich suche.
Eine Formel für 3.
Das man, bei zwei gegebenen Werten, den dritten (fehlenden) Wert berechnen kann, ist mir klar. Aber dafür muss man die Formel nach dem fehlenden Wert auflösen oder umformen. Und daran scheiterts halt bei mir im Moment (für 3.).
Und mag ja sein, dass jedem Mathematiker die Partialsumme der geometrischen Reihe geläufig ist. Mir als Hobby-Mathematiker ist der Ausdruck neu. Deshalb frag ich ja in einem Matheforum. Aber danke für das Stichwort.
Gruß
Martin
Aehm, also B aus S und n berechnen geht (im allgemeinen) geschlossen nicht. Aber ich helfe natürlich trotzdem mit der folgenden Erkenntnis:
x^n + ... + x^1 - S = 0
Sieht aus wie ein Polynom, oder? Für ganz kleine n (1, 2, 3 und 4) kann man da sicher was hinschreiben, Stichwort: pq-Formel, Cartanische Formeln, biquadratische Gleichung.
Für n >= 5 entdeckst Du gerade das Problem der Auflösbarkeit wieder (Auflösbare Gruppe – Wikipedia), was letztlich zur Formulierung der Gruppentheorie geführt hat. Die Unmöglichkeit kann ich hier nicht kurz und knapp darstellen, ist aber sehr interessant.