Ein Mann kauft in einem Supermarkt 4 Tafeln Schokolade.
Die Preise sind verschieden vo DM 0,-.
Eine kleine Sache gibt es zu beachten: Alle Tafeln kosten
addiert DM 7,77 und multipliziert ebenfalls DM 7,77
und sind natürlich auch in DM ausgezeichnet…
Welche Einzelpreise haben die Tafeln?
ICH bin der Ansicht, diese Aufgabe ist nicht lösbar.
Wie seht ihr das?
Lösung: 0,8; 1,25; 2,22 und 3,5
ICH bin der Ansicht, diese Aufgabe ist nicht lösbar.
Wie seht ihr das?
Hallo
Immerhin hast du 2 Gleichungen mit 4 Unbekannten. Das heißt, daß du dir 2 Lösungen vorlegen kannst und die anderen beiden kannst du dann ausrechnen.
Das Produkt der Zahlen muss 7,77 ergeben; die Primzahlzerlegung von 777 ist:
777=7*111
leider führt das nicht zum Ziel, also probiert man mal
7/2 und 111*2,
also:3,5 DM und 2,22 und zum Glück führt das dann zum Ziel!
Gruß
OLIVER
Hallo, Oliver,
jetzt muß ich aber ein bissel mit Dir schimpfen.
Es ist seit langem guter Stil hier im Rätselbrett, Lösungen nicht im Titel von Postings zu schreiben und auch wenn die Lösung im Text steht darauf hinweisen.
Schließlich wollen wir ja alle mal ne Chance haben das Rätsel selbst zu lösen.
Übrigens steht die Lösung auch seit geraumer Zeit schon im Archiv. Das Rätsel (welches eigentlich nicht) war nämlich schonmal da.
Gruß
Eckard.
Das Thema ist uralt, das Rätsel war iirc mal vor 30 Jahren im sommerrätsel in der süddeutschen Zeitung.
was mich interessiert ist, ob jemand eine Lösung hat, die nicht im „Ausprobieren aller Möglichkeiten“ besteht, idealerweise sogar so übersichtlich ist, daß sie auch ohne Computerhilfe nachvollzogen werden kann.
Das Rätsel krankt daran, dass man Geldbeträge nicht miteinander multiplizieren kann, weil dann Quadrateuro, Kubikcent oder Rubeldollar bei herauskommen.
Außerdem hängt das Ergebnis davon ab, ob man in der Währungseinheit oder der Scheidemünze rechnet.
10 Cent * 10 Cent = 100 Cent²
0,1 € * 0,1 € = 0,01 €²
10 Cent * 0,1 € = 1 Cent€
Das interpretierst du hinein., In der Originalversion ist viel wichtiger, daß die Preise mit einem Festkommarechner addiert/multipliiziert werden. Der Rest ist Illustration.
Vielleicht wurde die Frage deswegen schon vor über 21 Jahren gestellt.
Aber mich interessiert das Problem, weil ich bis heute keinen handlichen Lösungsweg gefunden habe.
Hallo @detlef2,
die Erklärung von @KeinesHerrenKnecht ist schon wichtig, weil das Rätsel nur funktioniert, wenn du die vorgegebene Zahl 7,77 in der gegebenen Währung belässt. Weiter oben hat jemand die Lösung
0,8; 1,25; 2,22 und 3,5
angegeben. Man kann natürlich sofort nachrechnen, dass diese Lösung stimmt. Man darf die Zahlen aber nicht z.B. in Cent umrechnen, also 80; 125; 222 und 350 daraus machen. Deren Summe ergibt zwar korrekt 777, aber das Produkt ist offensichtlich viel größer.
Diese oben angegebene Lösung basiert auf der folgenden Idee: Die Zahlen 2.22 und 3.5 ergeben das korrekte Produkt, 2.22 x 3.5 = 7.77, aber die zu niedrige Summe 2.22 + 3.5 = 5.72, also 2.05 zu wenig. Die beiden anderen Zahlen müssen also so gewählt werden, dass ihr Produkt Eins ergibt und ihre Summe den Fehlbetrag von 2.05. Damit sind diese beiden Zahlen aber schon eindeutig bestimmt. Das Produkt ist nämlich genau dann gleich Eins, wenn die eine Zahl der Kehrwert der anderen Zahl ist. Nennen wir die Zahlen also z.B. a und 1/a. Die Summe ist auch bekannt, nämlich a + 1/a = 2.05. Das lässt sich leicht in eine quadratische Gleichung umstellen und führt genau auf die beiden Lösungen 0.8 und 1.25.
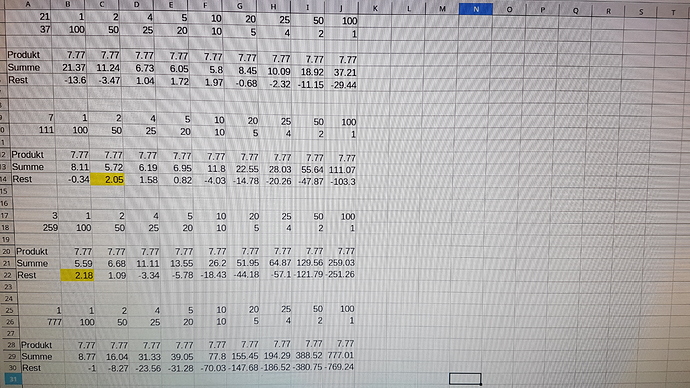
Man kann sich nun fragen, wie die vier Zahlen der Lösung gefunden wurden. Das ist oben in dem Beitrag angedeutet, man schreibt 7.77 = 777/100 und zerlegt Zähler und Nenner geeignet. Bei der Lösung wurde nämlich in
7.77 = 777/100 = (111 x 7) / (50 x 2 ) = 111/50 x 7/2 = 2.22 x 3.5
zerlegt. Daraus ergibt sich sofort die Idee, dass man die Zahlen 777 und 100 ja auch anders zerlegen kann. Wir finden natürlich schnell
777 = 1 x 777 = 3 x 259 = 7 x 111 = 21 x 37
100 = 1 x 100 = 2 x 50 = 4 x 25 = 5 x 20 = 10 x 10 = 20 x 5 = 25 x 4 = 50 x 2 = 100 x 1.
Wenn wir nun im Zähler 4 Zerlegungen und im Nenner neun Zerlegungen haben, dann ergeben sich daraus 4x9 = 36 verschiedene Kombinationen, die alle untersucht werden müssen. (Diese Untersuchung ist als Bild unten angehängt.)
Jede dieser Kombinationen führt auf zwei Zahlen mit dem korrekten Produkt von 7.77 und der falschen Summe. Es bleibt also jedesmal eine Differenz d übrig. Die beiden anderen Zahlen sind dann nach der obigen Überlegung die Lösung der quadratischen Gleichung a+1/a = d, nämlich
a1 = [d+sqrt(d^2-4)]/2 und a2 = [d-sqrt(d^2-4)]/2.
Aus der Aufgabenstellung ist sowieso klar, dass nur Kombinationen mit d>0 gesucht werden. Man sieht anhand der beiden Lösungen für a1 und a2 auch sofort, dass sogar d>2 sein muss.
Die 36 Kombinationen lassen sich natürlich leicht mit einer Tabellenkalkulation untersuchen. Dann findet man tatsächlich genau zwei Kombinationen, welche die Bedingung d>2 erfüllen, nämlich die schon oben angegebenen Zahlen 2.22 und 3.5 sowie neu dazu auch noch 3 und 2.59, bei denen sich ein Fehlbetrag von 2.18 ergibt. Die quadratische Gleichung führt dann auf die beiden etwas unhandlichen Lösungen
a1 = [ 109+3xsqrt(209) ]/100 und a2 = [ 109-3xsqrt(209) ]/100.
Wenn man diese Zahlen rundet, erhält man die vier Zahlen 0.656, 1.525, 2.59 und 3. Die Aufgabenstellung legt nahe, dass nur Lösungen gesucht werden, bei denen die Zahlen maximal zwei Nachkommastellen haben. Dann ist die oben vor 21 Jahren gepostete Lösung tatsächlich (und jetzt erwiesenermaßen 
) die einzige Lösung, bei der zwei Zahlen das Produkt Eins ergeben.
Nun mag jemand anderes untersuchen, ob es vielleicht noch weitere Lösungen ohne diese Einschränkung gibt.
Liebe Grüße
vom Namenlosen
Hallo!
Ich hatte mal mittels Bruteforce einfach alle denkbaren Kombinationen ausprobiert.
Die hier bereits genannte Lösung ist tatsächlich die einzige, aber das wissen wir inzwischen ja schon.
Da Kommazahlen immer ein wenig speziell für den Computer sind, gehen wir mal von Mark zu Pfennig über. Die Summe muss nun 777 betragen, das Produkt 777.000.000 (=7,77*1004)
Das Programm unten ist in Python geschrieben. Mag nicht das schnellste sein, aber naja…
Es gibt zwei Optimerungen:
Sicherlich kann man sich austoben und noch mehr Optimierungen einbauen, aber die 254 Sekunden sind schon OK.
import time
start=time.time()
sum=777
prod=777000000
for a in range(1,777):
print("a=",a) # Nur, um den Fortschritt zu sehen...
for b in range(a,777):
bsum=a+b
bprod=a*b
if(bsum >= sum or bprod >=prod):
break
for c in range(b,777):
csum = bsum + c
cprod = bprod * c
if (csum >= sum or cprod >= prod):
break
for d in range(c,777):
dsum = csum + d
dprod = cprod * d
if (dsum > sum or dprod > prod):
break
elif( dsum == sum and dprod == prod):
print("Treffer:",a,b,c,d)
print("Dauer:", time.time()-start)
Die Ausgabe ist:
a= 1
a= 2
a= 3
...
a= 80
Treffer: 80 125 222 350
a= 81
a= 82
a= 83
...
a= 776
Dauer: 254.68
Und daß man 2,77 als 2,22 * 3,5 darstellen kann ist dann eine Eingebung?
Hallo @detlef2,
man schreibt 7.77 als 777/100 und zerlegt sowohl die 777 als auch die 100 in jeweils zwei Faktoren. Dabei ergeben sich genau die 36 Möglichkeiten, die ich oben in der Tabelle zusammengeschrieben habe. Die gelb markierte 2.05 gehört zu der Kombiniation 777 = 7 x 111 und 100 = 2 x 50, also 7.77 = (7/2) x (111/50) = 3.5 x 2.22.
Liebe Grüße
vom Namenlosen
Sehr schön, @sweber!
Hier kommt noch eine optimierte Version in C++. Ich habe die Schleifen für a und b nach oben begrenzt und d aus a,b,c berechnet. Das Programm läuft in Sekundenbruchteilen, sodass man auch mal mit größeren Beträgen als 7.77€ experimentieren kann.
Liebe Grüße
vom Namenlosen
#include <iostream>
#include <iomanip>
#include <math.h>
#include <chrono>
#include <ctime>
int main(int argc, char **argv){
auto start_time = std::chrono::system_clock::now();
long SUM = 777; // Gesamtpreis in Cent SUM = a+b+c+d
long PROD = SUM*(long)pow(10,6); // PROD = a*b*c*d in Cent^4
for( long a=1; a<=1+SUM/4; a++ ){
for( long b=a+1; b<=1+SUM/2; b++ ){
for( long c=b+1; c<=SUM; c++ ){
long d = SUM-a-b-c;
if( d<c ){ break; }
if( a*b*c*d == PROD ){
std::cout << "\n" << a << " " << b << " " << c << " " << d << "\n";
}
}
}
}
auto end_time = std::chrono::system_clock::now();
std::chrono::duration<double> elapsed_seconds = end_time - start_time;
std::cout << std::setprecision(3);
std::cout << "\n\n elapsed time: " << elapsed_seconds.count() << "s\n\n";
return 0;
}Auch gut!
Das erinnert mich ein wenig an einen Prof, der und als Übungsaufgabe das Programmieren einer Simulation aufgegeben hat, und uns ermahnte, frühzeitig anzufangen - die Simulation benötige mehrere Stunden zum Laufen.
Gut, er machte alles mit Mathematica o.ä., während ich das in C (oder war’s noch Basic?) mit jeder Menge Optimierungen gemacht hab. Das lieft dan schon so seine… 0,37s.
Warum 2? Und nicht etwa 4?
Mir geht es darum, einen einfachen Zugang dazu zu kriegen, bevrorzugt sogar ohne Rechnerhilfe. Brute Force geht immer, aber die Probleme mit dem Gleichheitszeichen bei real numbers wurde schon angesprochen, bei integers muß ich auch an den Zahlbereich denken - die Aufgabe ist 30 Jahre alt (oder älter?) , damalige Heimcomputer hatten mit ihrem spielzeug basic oder spielzeug pascal nicht notwendig 32 bit integers, aber auch damals sollte sie lösbar sein.
Am schicksten fände ich eine Lösung „auf Papier“, Einstein wird nachgesagt, er hätte gerne auf alten Briefumschlägen gerechnet.
Hallo @detlef2.
Am schicksten fände ich eine Lösung „auf Papier“, Einstein wird nachgesagt, er hätte gerne auf alten Briefumschlägen gerechnet.
Was fehlt dir denn an der Lösung, die ich oben aufgeschrieben habe? Sie benutzt ausschließlich elementare Mathematik, reduziert das Problem auf 36 einfache Kombinationen und findet darunter zwei Lösungen, eine in ganzen Pfennigen und eine mit Wurzeln. Mit weniger Erklärungen und unter Verwendung der Vorder- und Rückseite hätte das auch auf Einsteins Briefumschlag gepasst.
Liebe Grüße
vom Namenlosen
Hihi. Das erinnert mich wiederum daran, dass mein Physik-Lehrer ein Programm entwickelt hatte, das das Interferenzmuster einer Doppelspaltanordnung (also aus Abstand, Breite, Entfernung der Lichtquelle usw.) berechnen konnte. Am Anfang einer samstäglichen Doppelstunde angeworfen, spuckte es kurz vor der Pause das Ergebnis aus. In welcher Sprache das geschrieben war, weiß ich nicht mehr sicher, aber ich meine, es wäre PASCAL gewesen. Die Software lief auf einem IBM-PC mit 8086er oder 8088 (wahrscheinlicher wg. 8 Bit) Prozessor.
Ich nahm den Code mit nach Hause und übertrug ihn mehr oder weniger 1:1 in das Omikron Basic meines Atari ST. Der einzige konzeptionelle Unterschied war, dass ich die Variablen als Konstanten setzte, d.h. bei Veränderungen in den Code eingreifen musste.
Tja, was soll ich sagen: mein Programm lief in knapp 2 Minuten durch. Hat mir nix gebracht, außer Spaß. Ich meine sogar, dass ich für die Demonstration das ganze Geraffel nebst Monitor einmal in die Schule geschleppt habe.