Hallo zusammen
Bei Folgender Aufgabe habe ich zwar die Lösung, aber der Lösungsweg ist mir nicht ersichtlich.
Die Ausgangstabelle:
Hier die Frage mit der Lösung:
Wäre froh um eine einfach Schritt-für-Schritt Erklärung
Vielen Dank
Preston
Hallo Preston,
ich gehe davon aus, dass die Erlösminderungen kein fester Betrag sind, sondern 2 % vom Bruttoerlös bei allen Produkten (zumindest kommt das heraus) und die variablen Kosten und Produktefixkosten ein fester Betrag sind.
Gäbe es keine Erlösminderung, müsstest du nur den DB II von 343.900 auf den Bruttoerlös von 12.000.000 aufschlagen.
Der DB II ist also schon um 2 % Erlösminderung gekürzt, also nur noch 98 %. Darum müssen die 343.900 : 98% x 100 % (oder einfach „: 0,98“) genommen werden und man kommt auf 350.918,37.
Wenn man diesen Betrag zum Bruttoerlös von 12.000.000 addiert, kommt man auf einen Bruttoerlös von 12.350.918,37.
Bruttoerlös 12.350.918,37
./. Erlösminderung 247.018,37
2,00%
Nettoerlös 12.103.900,00
Variable M-Kosten 3.000.000,00
Variable F-Kosten 7.150.500,00
DB I 1.953.400,00
Produktefixkosten 1.953.400,00
DB II 0,00
vorformatierten Text mit 4 Leerzeichen einrücken
Viele Grüße
Karin
Hallo Karin
Sorry, ich habe die entsprechende Angabe (2% Erlösminderungen) vergessen in die Aufgabe einzufügen.
Vielen Dank für deine Erklärung, ich kann sie sehr gut nachvollziehen. Was mich ein wenig verwirrt, ist dass du auf eine andere Lösung kommst (12’350’918,37 anstatt 14’566’741 wie in der Musterlösung).
Was ist dort schief gelaufen? Mit 14’566’741kommt man ja auch gar nicht auf einen DBII von 0?
Vielen Dank
Preston
Hi Preston,
ich habe einen Denkfehler gemacht bzw. die Lösung nicht beachtet. Ich hab gedanklich nur den Bruttoerlös erhöht, in deiner Lösung soll aber der Bruttoerlös durch Mehrverkauf erreicht werden. Und damit steigen natürlich die variablen Material- und Fertigungskosten.
Nachdem die Erlösminderung auch variabel ist, kann ein Prozentsatz gebildet werden, um die variablen Kosten darzustellen - eben die 13,41 % auf den Bruttoerlös.
Und die Formel für den Break-Even - also den Punkt, an dem weder Gewinn noch Verlust gemacht wird - lautet:
Break-Even-Umsatz = U BEP = K f : DBU
U BEP = kritischer Umsatz am BEP (Break-Even-Point)
K f = fixe Gesamtkosten (= 1.953.400)
DBU = Deckungsbeitrag des Umsatzes in Dezimalform (13,41 %)
Jetzt klar? Sonst stell ich morgen nochmal die Rechnung rein.
Viele Grüße
Karin
Sonst stell ich morgen nochmal die Rechnung rein.
Da wäre ich nicht abgeneigt. 
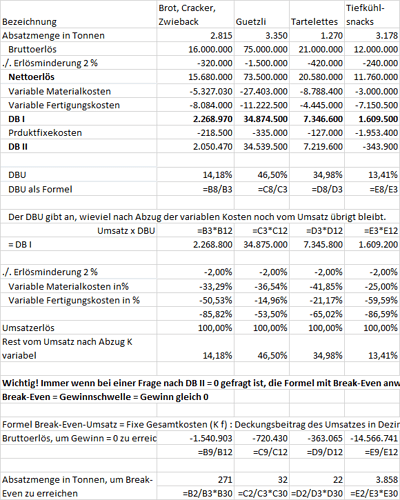
Bezeichnung Brot, Cracker, Zwieback Guetzli Tartelettes Tiefkühl-snacks
Absatzmenge in Tonnen 2.815 3.350 1.270 3.178
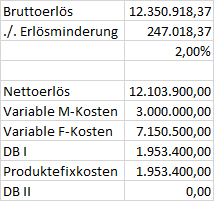
Bruttoerlös 16.000.000 75.000.000 21.000.000 12.000.000
./. Erlösminderung 2 % -320.000 -1.500.000 -420.000 -240.000
Nettoerlös 15.680.000 73.500.000 20.580.000 11.760.000
Variable Materialkosten -5.327.030 -27.403.000 -8.788.400 -3.000.000
Variable Fertigungskosten -8.084.000 -11.222.500 -4.445.000 -7.150.500
DB I 2.268.970 34.874.500 7.346.600 1.609.500
Prduktfixekosten -218.500 -335.000 -127.000 -1.953.400
DB II 2.050.470 34.539.500 7.219.600 -343.900
DBU 14,18% 46,50% 34,98% 13,41%
DBU als Formel =B8/B3 =C8/C3 =D8/D3 =E8/E3
Der DBU gibt an, wieviel nach Abzug der variablen Kosten noch vom Umsatz übrigt bleibt.
Umsatz x DBU =B3B12 =C3C12 =D3D12 =E3E12
= DB I 2.268.800 34.875.000 7.345.800 1.609.200
./. Erlösminderung 2 % -2,00% -2,00% -2,00% -2,00%
Variable Materialkosten in% -33,29% -36,54% -41,85% -25,00%
Variable Fertigungskosten in % -50,53% -14,96% -21,17% -59,59%
-85,82% -53,50% -65,02% -86,59%
Umsatzerlös 100,00% 100,00% 100,00% 100,00%
Rest vom Umsatz nach Abzug K variabel 14,18% 46,50% 34,98% 13,41%
Wichtig! Immer wenn bei einer Frage nach DB II = 0 gefragt ist, die Formel mit Break-Even anwenden.
Break-Even = Gewinnschwelle = Gewinn gleich 0
Formel Break-Even-Umsatz = Fixe Gesamtkosten (K f) : Deckungsbeitrag des Umsatzes in Dezimalform (DBU)
Bruttoerlös, um Gewinn = 0 zu erreichen -1.540.903 -720.430 -363.065 -14.566.741
=B9/B12 =C9/C12 =D9/D12 =E9/E12
Absatzmenge in Tonnen, um Break-Even zu erreichen 271 32 22 3.858
=B2/B3B30 =C2/C3C30 =D2/D3D30 =E2/E3E30
Rückmeldung, ob es dir jetzt klar ist, wäre nett.
Hallo Karin
Vielen Dank für deine Erklärung. Klarer als vorher ist es auf jeden Fall. Ich weiss jetzt was ein DBU ist und wie man ihn ausrechnet.
Was ich noch nicht ganz verstehe ist diese Formel:
Formel Break-Even-Umsatz = Fixe Gesamtkosten (K f) : Deckungsbeitrag des Umsatzes in Dezimalform (DBU)
Warum nimmt man die Fixkosten?
Hi Preston,
auf YouTube gibt es schöne Tutorials, die den Zusammenhang Deckungsbeitrag / fixe Kosten / variable Kosten ganz gut erklären.
Hier z. B.
Danach sollte dir die Herleitung dieser Formel verständlich sein. Dürft ihr keine Formelsammlung benutzen?
Karin
Hallo Karin
Vielen Dank für deine Hilfestellung, meine Frage(n) sind beantwortet
Nein, mit Formelsammlung ist nix 
