Dreieck mitSeitenhalbierenden

Wissenschaft Mathematik
#1

Datei 17.07.17, 10 55 15
Datei 17.07.17, 10 55 152048×1536 232 KB

hallo zusammnen

wer hilft mir,folgendes Dreieck zu zeichnen:
c = 7 cm
sa = 6 cm : Seitenhalbierende von Punkt A in der Stecke BC. Schnittpunkt S
Gamma: 70 Grad

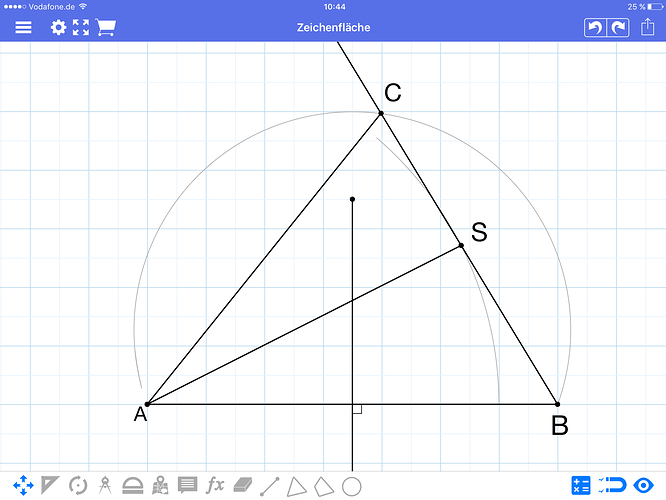
hier: Die Strecke AB habe ich „nur so“ gezeichnet, weil ich sie ja nicht kenne.

Also: Inenkreiswinkel zeichnen für gamma = 70 Grad ist keine Sache.
Ausgrechnen ginge eigentlich auch, nur ich lande bei Gleichungen 4. Grades.
Die kann ich nicht lösen bzw hab ich keinen Bock drauf.
Meine Geleichungssysteme sind
6² = b² + (1/2a)² - 2b1/2acos 70
und
7² = b² + a² - 2ba*cos 70

mit auslösen und gleichsetzen komme ich nicht klar wegen 4. Grades.
daher zeichnen!
aber wie??

vielen Dank schon mal im voraus

#2

Wo ist c in der Skizze?

#3

Mit c ist klein c gemeint, also die streck AB.
C= 7 cm

#4

Aus deinen Vorüberlegungen entnehme ich, daß die Aufgabe nicht ausschließlich graphisch gelöst werden soll.

Also kannst du den Umkreisradius berechnen:

rUmkreis = c/2sinγ (← Sinussatz)

Mit c= 7,0 und γ = 70° → rUmkreis = 3,725

Ich verwende die üblichen Bezeichnungen:
Winkel γ liegt bei C
c = AB
b = BC

Kreis mit Radius rUmkreis um A oder B schneidet mc (= die Mittelsenkrechte auf c) im Umkreismittelpunkt MUmkreis

Kreis um MUmkreis mit rUmkreis ergibt den Umkreis kUmkreis, auf dem C liegen muß.

Den Kreis um A mit rSeitenhalbierende = 6 hast du bereits. Auf ihm liegt per def. irgendwo der der Seitenmittelpunkt S,

S ist per def. zugleich der Fußpunkt der Mittelsenkrechten auf b. Ich nenne ihn jetzt besser Mb. Er liegt damit auf dem Thaleskreis über der Strecke BMUmkreis und ist damit zugleich der Schnittpunkt dieses Thaleskreises mit dem Kreis um A mit rSeitenhalbierende. Damit ist Mb festgelegt.

Die Gerade durch B und Mb schneidet den Umkreis kUmkreis im Punkt C. Fertig.

Zur Prüfung der graphischen Konstruktion: Die Strecke BMb sollte natürlich nun dieselbe Länge haben wie CMb.

Gruß
Metapher

#5

addendum

Du kannst, wie mir gerade einfällt, die Aufgabe natürlich doch komplett graphisch lösen, und zwar mit dem → Umfangswinkelsatz:

Du trägst an mc (= der Mittelsenkrechten auf c) in irgendeinem Punkt P den Winkel γ ab, und verschiebst den freien Schenkel parallel, bis er den Punkt B trifft. Der entsprechende Punkt P’ auf mc ist dann MUmkreis. Du brauchst also den Umkreisradius gar erst nicht zu berechnen.

#6

Hi Metapher
Danke für die Information.
Die seitenhalbierende ist auch die mittelsenkrechten.
Das ist neu für mich gewesen, aber scheint plausibel zu sein.
Auf jeden Fall führt das weiter.
Morgen gehe ich da weiter dran.

Rechnerisch kommst du auch auf eine Gleichung 4. Grades.
Berechnest du auch gerne Dreiecke?

Habe da noch eine neue Aufgabe in der Pipeline

Mehr dann
Ralf

#7

Oh nein, keineswegs. Aber der Fußpunkt der Seitenhalbierenden ist ja der Mittelpunkt der gegenüberliegenden Seite - deshalb heißt sie ja „Seitenhalbierende“. Und die Mittelsenkrechte startet ebenfalls genau in diesem Punkt - deshalb heißt sie ja „Mittelsenkrechte“.

#8

sorry, vertippt:

das

b = BC

ist natürlich Unsinn. Vielmehr gilt

a = BC

Entsprechend heißt der Seitenmittelpunkt auf a, um den es hier ja vorzugsweise geht, Ma (= S) und nicht Mb.

#9

vielleicht hast du ja etwas verwechselt:

Kleinbuchstaben = Strecken bzw. Linien bzw. Seiten.
Großbuchstaben (und fett) = Punkte. Wobei z.B. AB = die Strecke zwischen A und B (also c)

#10

Mist, sehe ich hier gerade meine Fehler:
" nur so" habe ich die Strecke BC also a gezeichnet.

Sorry für meine Unkorrektheiten

LG Ralf

#11

Hi, kein Problem. Hab mich ja auch vertippt und zu spät bemerkt.

Und? Konntest du meine Konstruktionsbeschreibung nachvollziehen?

#12

Hallo Metapher
Shit Happens

Auf ein neues .
Ich gebe bald eine saubere Zeichnung rein verbunden mit einer neuen Rechnung, mit der ich nicht klar komme.

c = 7 cm ( Streck A B)
Gamma = 70 grad
Winkelhalbierende von A wa= 6 cm

Wie zeichnen?
Wie rechnen?

Skizze bastel ich später noch mal rein.
Satz des apollonius muss ich wohl anwenden.

Viel Vergnügen erstmal damit.
Vielleicht kommst du weiter​:smiling_imp::smiling_imp::smiling_imp::smiling_imp:

Ralf

#13

Der Satz des Apollonios (sic!) hat mit Winkelhalbierenden nichts zu tun.

Ich denke, daß es bei deiner Aufgabensammlung um geometrische Konstruktionen (Zirkel, Lineal, Winkelmesser) geht und nicht um Berechnungen.

Und denk daran, daß hier nicht das Denksportaufgabenbrett ist. Nicht, daß es vom Mod was mit dem Nudelholz auf den Kopp gibt :wink:

Du hast meine letzte Frage noch nicht beantwortet

Gruß
Metapher