Dreiecksberechnung

[ralf_g_nther]

Hallo zusammen

Selber habe ich mich in
eine eigene Aufgabe reingeritten und komme nicht daraus.

Zeichnen kann ich es,aber nicht berechnen . . .

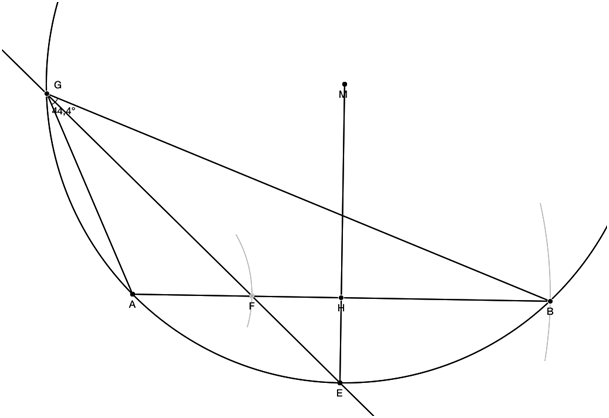
Worum geht’s :

Um ein Dreieck A,B,G (den Buchstaben C habe ich nicht
eingeben können)

Gegeben c = 7 cm

Umkreiswinkel r= 5 cm

Winkelhalbierende GF schneidet c im Verhältnis 2/5.

G bekommt man über den Südpolsatz , die Verlängerung von E und F.

Den Winkel Gamma geht über halber Mittelpunktswinkel gleich Umkreiswinkel mithilfe

des kleinen sinussatzes.

Im Dreiech A M H gilt demnach Sinus
Gamma= ½ c/r

                                                      Sinus Gamma = 3,5/5

                                                           
               = 0,7

=>Gamma = 44 grad

Soweit so gut, aber wie berechne ich die Seite a und b???

Satz des Apollonius hilft mir nicht weiter. . .

Wer kann helfen??

LG

Ralf

Bild folgt auf der zweiten Seite; ich hoffe es ist dabei. .
.

[nudltrudl]

ich werde das Gefühl nicht los, dass da noch ein paar Angaben fehlen.

[ralf_g_nther]

Wieso?
Du zeichnest zuerst den Kreis mit r=5 cm
Danach trägst du die Sehne an mit 7 cm. Die Sehne teilst du durch 7 bzw stellst das Verhältnis 2 zu 5 dar.
Mit der mittelsenkrechten der sehne, die natürlich auch durch den Mittelpunkt geht , erhältst du E.
Verbinde E mit der sehneneiteilung von 2/5 erhältst du G ( Buchstabe C könnte ich nicht eintippen) das ist der Südpolsatz .

Damit hast du alle 3 Punkte des Dreiecks . . .

Aber die Berechnung fehlt mir.

LG

[Martin]

Hallo Ralf,

vorab das Ergebnis, danach die Herleitung:

a = c / sqrt(τ² – 2τ cos γ + 1)
b = c / sqrt((1/τ)² – 2/τ cos γ + 1)

(Numerisch: γ = 44.427004°, a = 9.12339099166, b = 3.649356396664)

mit
τ = 2/5 = 0.4 (Erklärung s. u.)
und
cos γ = sqrt(1 – (c/(2r))²)

Das Dreieck ΔABC wird durch die C-Winkelhalbierende in zwei Teile, nämlich ΔAFC und ΔFBC zerlegt. Es sei w := |CF| und p := |AF| und q := |FB|. Notiere für die Teildreiecke jeweils einmal den Sinussatz (w/… = p/… bzw. w/… = q/…) und folgere daraus die Identität

sin(α) / sin(β) = q/p

Ich kürze p/q zu τ (griechischer Buchstabe „tau“) ab. Der Parameter τ enthält die Information darüber, wie F die Dreieckseite c teilt. In Deinem Beispiel hat τ den Wert 2/5.

Über α + β + γ = π drückst Du jetzt β durch α aus und erhälst

sin(α) / sin(α + γ) = 1/τ

Bringe sin(α + γ) auf die rechte Seite und löse es in eine Summe sin cos + cos sin auf. Anschließende Division durch cos α liefert Dir tan α als neue Unbekannte. Auflösung der Gleichung nach tan α ist simpel. Resultat:

tan(α) = sin(γ) / (τ – cos(γ))

tan β ergibt sich daraus sofort aus Symmetriegründen (Vertauschung von p und q macht τ zu 1/τ) zu:

tan(β) = sin(γ) / (1/τ – cos(γ))

Für die Seitenlängen a und b bemühst Du wiederum den Sinussatz – diesmal für das „ganze“ Dreieck, also ΔABC:

a = c sin(α) / sin(γ)
b = c sin(β) / sin(γ)

Über die Beziehungen sin = tan / sqrt(1 + tan²) und cos = sqrt(1 – sin²) kannst Du das dann schlussendlich zu meinen eingangs angegebenen Gleichungen weiterverrechnen.

Alles klar? :–)

Schönen Sonntag
Martin

[ralf_g_nther]

Danke für den schönen Sonntag; da hast du es mir richtig „besorgt“.
OK, werde mir das in hoher Erwartungshaltung reintuen und meinem Verständnis zuführen.

danke trotzdem für deine Bemühungen.

Dreiecksberechnungen machen mir halt spass, auch wenn das mal durch die Hirnklappen geht . . .

so long

Ralf

[ralf_g_nther]

Irgendwie habe ich da einen Durchhänger.
Wenn ich so popelige Dreiecke zeichnen muss wie: c= 7 cm. hc=4 cm und Gamma =40 grad , dann klappt die Zeichnung. Nur die Berechnung von Seite a und b funzt nicht grrrrh.

Zeichnung hierzu Versuch ich anzuhängen.
Geometrie pad ist da ein wenig bockig.

VersendeVersenden

[Martin]

Hallo,

c= 7 cm. hc=4 cm und Gamma =40 grad

das ist meines Erachtens auch keine ganz simple Aufgabe.

Ich habe es über den Umkreisradius r und die Fläche (!) F des Dreiecks gelöst. An diese beiden Größen kommt man nämlich leicht heran: r = c/(2 sin γ) und F = 1/2 c h_c. Weil nun r und F noch über die Formel r = a b c/(4 F) miteinander verknüpft sind, ist es möglich, das Produkt a b zu berechnen:

a b = … = c h_c/sin γ

Damit ist schonmal eine gute (aber natürlich noch nicht zur Lösung ausreichende) Information gewonnen. Eine zweite Gleichung für die beiden Unbekannten a und b ergibt sich aus dem Kosinussatz – er liefert die Information, wie groß a² + b² ist:

a² + b² = c² + 2 a b cos γ = … = c (c + 2h_c/tan γ)

Damit kennen wir also ab sowie a² + b² und müssen daraus nur noch a und b berechnen. Diesen Teil der Lösung überlasse ich Dir (für die richtige Interpretation des „±“ in der Mitternachtsformel beachte bitte, dass a und b in den Ausgangsgleichungen völlig symmetrisch auftreten).

Gruß
Martin