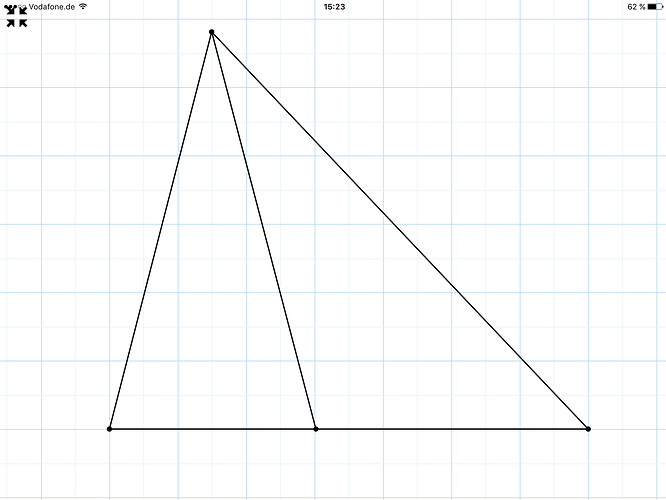
Ich habe da eine Sache:
Die Winkelhalbierende Gamma teilt c in 3 zu 4 aus.
Mit c = 7 cm
W Gamma = 6 cm
Durch hin und her rechnen komme ich auf a = 8 cm und b = 6 cm
Soweit so gut.
Damit kann ich nach dem rechne das Dreieck zeichnen.
Nur!
Wie kann ich das Dreieck vor dem berechnen zeichnen?
Wer hilft?
Die Buchstaben des Dreieck sind Pferde gegangen.
Es sind aber die " normalen" Bezeichnungen . . .
Also ich habe gerade mal mit einem Halbkreis um W, Radius 6 cm, angefangen und sehe sofort noch zwei andere Lösungen. Von daher ist entweder das Problem unterbestimmt oder ihr habt noch Kontext, den ich nicht habe.
Hallo hroptatyr ( Irrer Name . . . )
Wir haben normale dreiecksbeschriftung mit S als Schnittpunkt von w und c.
Dann habe ich 2 x den großen cosinussatz genommen über ACS und SCB.
3^2 = b^2 + 6^2- 2xbx6xcos gamma und
4^2 = a^2 + 6^2 - 2xax6xcos gamma
Nach cos gamma auslösen und gleichsetzen.
Ferner gilt ( Satz des Apollonius) b/3= a/4. also b=3/4a
Einsetzen!
=> a= 8 cm und b= 6 cm. ( das b auch 6 cm ist, ist wohl Zufall)
Von daher ist die Rechnung eindeutig, was du ja auch zeichnerisch nachvollziehen kannst.
Die gleiche Geschichte habe ich auch variiert und zwar so, dass w die Strecke c teilt in 2/5 ( im Punkt S)
Auch da funzt alles. (a= Wurzel 115 cm und b= Wurzel 18,4 cm)
Nur wie zeichne ich das V O R H E R!
LG
Ralf
