hi,
das ist so etwa die sinnloseste Ausrede überhaupt.
Es steht sogar dabei, dass die Lösung in der Aufgabe 8 zu finden ist.
Aufgabe 9 prüft nur, ob Aufgabe 8 verstanden oder abgeschrieben wurde.
https://www.lernhelfer.de/schuelerlexikon/physik/artikel/energieerhaltungssatz-der-mechanik
grüße
lipi
Das hängt vom Luftwiderstand ab; auch der ist oben und unten verschieden. Grund: Temperatur, rel. Feuchtigkeit, Barometerstand.
Das hängt kaum vom Luftwiderstand des Fahrzeuges (cw-Wert) ab.
Was nützt es dir hier eine Formel zu schreiben, da musst du dir schon deinen Kopf zerbrechen.
MfG
Wer ganz schlau sein will, sagt, die Aufgabe ist nicht lösbar, weil keine Angaben zur Reibung gemacht wurden. Das spart eine Stunde Arbeit, aber ob man damit beim Lehrer am Montag durchkommt?
Die minimale Geschwindigkeit ist in meinen Augen auch die, die unter optimalen Bedingungen gilt, also ohne Reibung und Luftwiderstand.
Dass ein Auto, was mit viereckigen Rädern im Honig fährt es veilleicht etwas schwerer hat, dürfte wohl klar sein …
Hallo,
ich werde dir hier Hinweise zur Lösung geben, aber nicht die Lösung selber!
Zu 9.1
Der Wagen hat nach der Fahrt eine bestimmte Lageenergie.
Er hat am Start sowohl eine dortige Lageenergie als auch zusätzlich eine Bewegungsenergie.
Da - diese Voraussetzungen nehme ich mal einfach an - Reibung vernachlässigt werden soll, kannst du eine einfache Formel aufstellen, die besagt:
Energie am Start = Energie am Ende.
In dieser Formel kommt als Unbekannte die Masse des Fahrzeugs vor, sie ist trotzdem lösbar, weil sich diese am Ende als nicht relevant herausstellen wird.
Zu 9.2
Hier hast du links am Start Lage- und Bewegungsenergie, die addiert die Energie des Fahrzeugs ergeben und rechts am Ende hast du nochmaln eine Summe aus diesen zwei Energieformen. Auch hier bekommt man eine Gleichung, wenn man einfach schreibt: Lagenergie1 + Bewegungsenergie1 = Lageenergie2 + Bewegungsenergie2
Was soll dieser Quatsch?
Es ist doch wohl eindeutig worum es bei der Aufgabenstellung geht. Dass es keine idealen Fahrzeug gibt, sollte doch jedem bekannt sein, dachte ich zumindest.
„mit welcher maximalSTEN Geschwindigkeit“ grins > Mathe ohne Deutschkentnisse
.
„finde nichts im Internet“ Was haben die Altvorderen eigentlich ohne Internet gemacht, vor 30 Jahren ? Sogar ohne Strom haben sie das schon gerechnet, vor 300 Jahren.
.
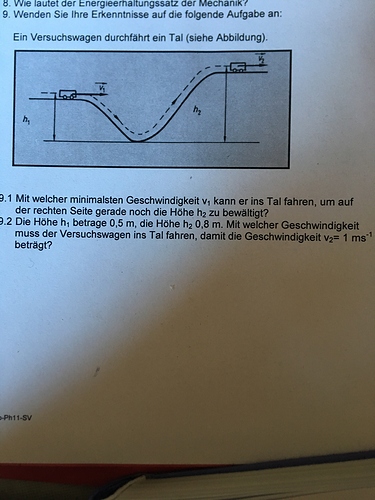
Die untere Haelfte des Frage-Bildes verbraucht nur Speicherplatz - sinnlos - kann weg
.
Der Hoehenunterschied vom Start bis zum Ziel hinauf braucht den Schwung auf,
wenn ohne Reibung und Luftwiderstand.
Unterwegs wird die Fuhre schneller, bergab, bis zu welchem Tempo ist doch die Frage, oder?
Jetzt das uebersetzen in Physik
Gruss Helmut
Energie im Tal ?
Alter des Fahrers ?
Gesucht ist nach meiner Meinung eine Geschwindigkeit, keine Energie.
Wer sich beim Lehrer noch unbeliebter machen will sagt, die Aufgabe sei allein schon deswegen nicht lösbar, weil keine Angaben zu Gravitation gemacht wurden 
Den Luftwiderstand ignorierend knallt das Fahrzeug nämlich selbstverständlich dem Vektor v1 folgend gegen die gegenüberliegende Felswand ;D
VG
J~
Die Energiedifferenz der Lageenergie ist gleich der minimalen kinetischen Energie bei h1, damit der Wagen bis zur Höhe h2 kommt.
Das Fahrzeug folgt zwar Vektor v1, aber - da keine Angaben über die elektromagnetische Wechselwirkung gemacht wurden - knallt nichts sondern es fliegt widerstandslos durch die Wand hindurch geradeaus weiter.
stimmt! Bestimmt ein Fahrzeug von dieser neumodischen Neutrino-Marke. Der Lehrer ist aber auch pfiffig solche fiesen Fragen zu stellen 
VG!
J~
Ich finde die Annahmen über Luftwiderstand, Gravitation usw. witzig. Es ist aber auch ein Lehrstück dafür, dass man bei jeder Aufgabe (auch in der Mathematik) nicht jede Voraussetzung der Aufgabe hinschreiben kann - dafür gibt es prinzipiell zu viele Möglichkeiten. Das Fahrzeug in der Aufgabe könnte z.B. in einer Flüssigkeit oder in einem überkritischen Gas auf dem Jupiter über eine klebrige Oberfläche fahrend verstanden werden, während seine Räder blockiert sind und es exotherm verbrennt. In der Mathematik kann man z.B. die genutzte Metrik beliebig umdefinieren. Man muss also recht viele Rahmenbedingungen als „Kommunikationsgrundlage“ voraussetzen und voraussetzen können, anders geht Aufgabenstellung nicht. (Trotzdem witzig :D)