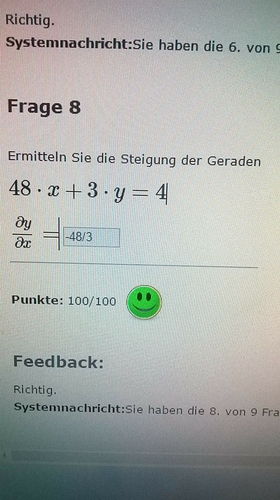
Kann mir jemand verraten wie das errechnet wurde?
Am besten einfach und übersichtlich, damit ich meine schwierigkeiten genauer ausdrücken kann. Vergesst nicht, ihr erklärt es nicht einem prof dr xy… Sondern nur mir… 
Moin,
was Du denn schon versucht?
Versuch die Gerade zu zeichnen!
Also y = …
Dann hast Du die Lösung vor Dir.
Hast Du beim Umformen Probleme?
Gruß Volker
48x + 3y = 4 …|-48x
=> 3y = 4 - 48x| /3
=> y = 4/3 - 48/3x (das ist dann die Geradengleichung)
Die Steigung ist also -48/3 (als dy/dx bzw. „dy nach dx“) .
Die Gerade geht durch den Punkt (0|4).
Hope it helps.
BigData
Ich schwöre euch… Soooo dooof bin ich garnicht… Dieser ausdruck links vor der lösung (@y@x)= hat mich dazu gebracht, nach einer lösung zu suchen, mit dem ableitungsverfahren…
Ich fühl mich schon einwenig behindi…
Danke jungs…
Boar wie affig… Ich hab versucht die gleichung erst auf y abzuleiten, dann geteilt durch ableitung x  …
…
Was bedeutet denn dieser besagte zeichen vor der lösung?
Hallo!
Du meinst das ∂ ?
In der Schule benutzt man für die Ableitung meist nur das Apostroph:
y’
Das ist OK, solange es in der Gleichung nur eine Variable gibt, oder man genau weiß, auf welche Variable man die ableitungsregeln anwenden soll. Gibt es mehrere Variablen, und man muß angeben, nach welcher man ableiten soll, schreibt man das als Bruch:
dy
—
dx
Und dann gibt es da noch
∂y
—
∂x
Der Unterschied zwischen d und ∂ ist klein, aber fein. Das d steht für die totale Ableitung, das ∂ für die partielle Ableitung.
Stell dir vor, du hast folgendes gegeben:
z=x²+y² und y=2x. Also im Prinzip nach dem Einsetzen z=5x².
Bei der totalen Ableitung dz/dx wird nach dem Einsetzen abgeleitet. Das Ergebnis ist also 10x.
Bei der partiellen Ableitung ∂z/∂x wird vor dem Einsetzen abgeleitet: Das Ergebnis ist da zunächst 2x+y², und nach dem Einsetzen dann 2x+4x².
Da bei dir nichts eingesetzt wird, spielt es keine Rolle, ob d oder ∂.
Die Gerade geht durch den Punkt (0|4/3).
Hallo,
Bei der partiellen Ableitung ∂z/∂x […] Das Ergebnis ist da zunächst 2x+y²
nein, nur „2x“. Weil alle anderen Variablen als die Differentiationsvariable bei der partiellen Ableitung als konstant betrachtet werden. – Einsetzen kannst Du dann hier freilich nix mehr, weil der Term kein y enthält.
Gruß
Martin
Wie recht du hast. Keine Ahnung, wie mir das passieren konnte.
Dann also eher so, wenn man noch was zum Einsetzen haben will:
z=x2 y2 mit y=2x. Nach dem Einsetzen: z=4x4
dz/dx=16x3
∂z/∂x=2x*y2, nach dem Einsetzen dann 8x3
Nanu? Inwiefern ist denn denn nun —>∂z/∂x=<— Version beim errechnen der Steigung in der obigen Aufgabe Nützlich?
richtig…hatte mich verschrieben
nochmals:
y = 4/3 - 48/3x
dy/dx (partiell…keine Computertaste) ist dann 48/3.
Im Prinzip gem. der Vorredner…
- 48/3 (Tippfehler)
…in Worten minus achtundvierzig drittel