Hallo
Was ist der imaginaere teil von exp(j(omega(t)+ phi)) und warum?
Omega ist die Winkelgeschwindigkeit
J ist die komplexe Zahl
Phi ist die phasenverschiebung
Danke
Das Ding heißt „imaginäre Einheit“ und wird mit einem kleinen „i“ dargestellt.
Die Eulersche Formel lautet
eiy = cos(y) + i sin(y),
für deinen Ausdruck gilt daher
ei(ω(t) + φ) = cos(ω(t) + φ) + i sin (ω(t) + φ)
Der Imaginärteil ist fettgedruckt.
1 Like
Danke
Aber, wenn ich z.b. die folgende kosinuswelle
V(t)= 220 V .cos(omeg.t+40)
In euelerform schreibe, bekomme ich
220 V.exp(j40)
Und omega t spielt dann keine Rolle
Hi!
U(t) = 220V * cos(w*t + 40)
hat mit Euler nichts zu tun.
Euler wäre
U(t) = 220V * exp(i*(w*t + 40))
= 220V * cos(w*t + 40) + i* 220V * sin(w*t + 40)
Hier ist U(t) eine komplexe Größe, und dann ist
Re(U(t))=220V * cos(w*t + 40)
Im(U(t))=220V * sin(w*t + 40)Danke
Ich meinte in polarform wuerde die Kosinuswelle so aussehen
220∠40
Omega.t spielt keine Rolle
Du hast recht, dass in Polardarstellung ein Kreis mit Radius 220V draus wird:
|U(t)| = 220V
Man muss allerdings im Hinterkopf halten, dass der Kreis daher kommt, weil für t beliebige Werte erlaubt sind. Fordert man t=0…90°, dann gibt das auch nur nen Viertelkreis. Sowas kann manchmal wichtig sein.
Hallo
Man betrachtet omega.t als komlex Deshalb fehlt es in Polarform. Ich verstehe es nicht, warum omega t komplex ist
Hi!
Es fehlt nicht in der Polarform, weil man es komplex betrachtet. Es fehlt, weil es in nem SIN und COS steht, und das dann nunmal einen Kreis ergibt.
Das mit den komplexen Zahlen in der E-Technik ist erstmal ein mathematischer Formalismus, der auf den ersten Blick keinen tieferen Sinn macht. Allerdings lassen sich damit viele Dinge zügig berechnen.
Du kennst sicher Widerstandsnetze, und durftest die bestimmt auch mal bis zum Erbrechen durchrechnen. Was würdest du tun, wenn da auch Spulen und Kondensatoren drin sind, und das ganze mit Wechselspannung betrieben wird? Interessanterweise kann man Ohm und Kirchhoff weiter verwenden, wenn man das mit der Phasenverschiebung zwischen Strömen und Spannungen hin bekommt. Und das gelingt, wenn man die Spulen als komplexe Widerstände Z=iwL und die Kapazitäten als Z=-i/(wC) schreibt.
Ganz einfaches Beispiel: Ne Spule an 230V, welcher Strom fließt? Zunächst gilt
Z = iwL = wL * exp(i * π/2)
Und jetzt Ohmsches Gesetz:
I = U / Z
= 230V * exp(iwt) / (wL * exp(i * π/2))
= 230V / (wL) * exp(i(wt-π/2))
= 0,73A * exp(i(wt-π/2))
Das ohmsche Gesetz liefert dir hier nicht nur den Strom, sondern gleich auch die Phasenverschiebung von π/2 (=90°).
OK, das hättest du auch so gewusst. Aber was wäre, wenn da noch R=100 Ohm in Serie ist?
I = U / (R+Z)
= 230V * exp(iwt) / (R + wL * exp(i * π/2))
= ...
= 230V / sqrt(R²+L²w²) * exp(i(wt-atan(Lw/R)))
=0,69A * exp(i(wt-1.26))
Zugegeben, die Rechnung ist sehr unangenehm, aber reine Fleißarbeit. Das lässt man besser den PC rechnen. Jedenfalls, neben dem Betrag des Stromes bekommst du hier auch wieder die Phasenverschiebung raus, der Strom eilt um 1,26rad=72,3° nach.
2 Like
Bei einer komplexen Zahl z mit der Darstellung z = a + i⋅b wird der reelle Koeffizient a als Realteil bezeichnet, der reelle Koeffizient b wird als Imaginärteil bezeichnet. Mit anderen Worten, die imaginäre Einheit i ist nicht Teil des Imaginärteils.
Das heißt in der folgenden Formel
ei(ω(t) + φ) = cos(ω(t) + φ) + i ⋅ sin(ω(t) + φ)
ist auf der rechten Seite der Realteil kursiv gesetzt, und der Imaginärteil ist fett gedruckt. Die imaginäre Einheit i gehört weder zum Real- noch zum Imaginärteil, und ist daher weder fett noch kursiv
1 Like
Hallo,
Und omega t spielt dann keine Rolle
wahrscheinlich hast Du ein Problem damit, zwischen der komplexen Größe und ihrer komplexen Amplitude zu unterscheiden.
Folgende Rechnung enthält praktisch alles, was es dazu zu sagen gibt (dass Dir die Beziehung eix = cos(x) + i sin(x) bekannt ist, setze ich mal voraus):
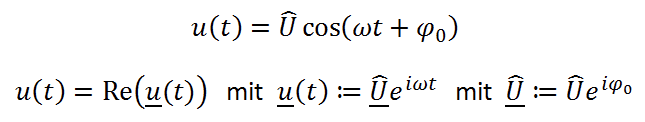
Darin ist u(t) die (reelle) Spannung, Û ihre (reelle) Amplitude, ω ihre Kreisfrequenz und ϕ0 ihr Nullphasenwinkel. Das cos-Argument ωt + ϕ0 hat auch noch einen Namen – das ist die Phase der Schwingung. Sie wächst zeitlich mit der konstanten Steigung ω an.
Das unterstrichene u(t) ist die komplexe Spannung und das unterstrichende Û ihre komplexe Amplitude (manchmal auch „Phasor“ genannt). Genauso wie die reelle Amplitude ist auch die komplexe Amplitude zeitunabhängig. Die reelle Spannung ergibt sich aus der komplexen Spannung durch Realteil-Bildung („Re“) ; die reelle Amplitude aus der komplexen Amplitude durch Betragsbildung.
Gruß
Martin
1 Like