Hallo!
Üblicherweise werden wir dir die Aufgabe hier nicht vorrechnen, denn dadurch lernst du ja nichts. Allerdings helfen wir dir hier gerne mit Hinweisen.
In der Überschrift schreibst du, das hier sei ein Extremwertproblem. Demnach musst du dir überlegen, welche Größe maximal oder minimal werden soll, und wie du diese Größe aus den Gegebenheiten berechnen kannst. Da gibt es mehrere Möglichkeiten.
Eine wäre:
Berechne für ein beliebiges α, wie lang die Länge l des Teils sein darf, damit es die obere Straßenbegrenzung so grade eben berührt. Es ist klar, dass das Teil für sehr kleine α und auch für α in der Nähe von 90° quasi unendlich lang sein darf, aber dazwischen gibt es ein Minumum. Also: Den Term für l nach α ableiten, und das Minumum suchen.
Eine andere:
Angenommen, das Teil hat eine (bisher unbekannte) Länge l. Dann kannst du für jedes α ausrechnen, wie weit das Teil nach oben ausschwenkt. Berechne das Maximum der Auslenkung durch Ableiten nach α. Anschließend forderst du, dass die maximale Auslenkung grade der Straßenbreite entspricht, und kannst so dann die Länge l berechnen.
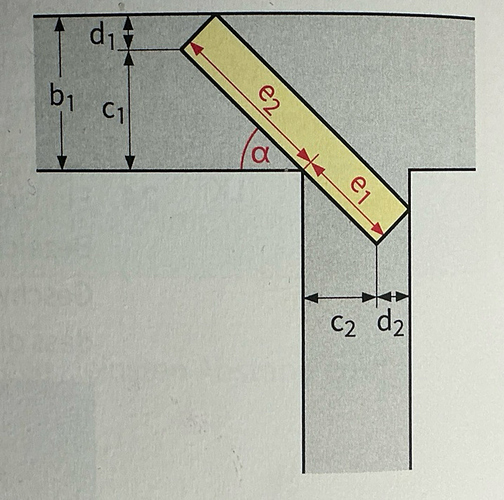
Ein wesentliches Problem dieser Aufgabe ist, wie du die benötigten Größen überhaupt berechnen kannst. Aber wenn du scharf hinschaust, gibt es ganz ganz viele rechtwinklige Dreiecke mit dem Winkel α, die dir massiv helfen.
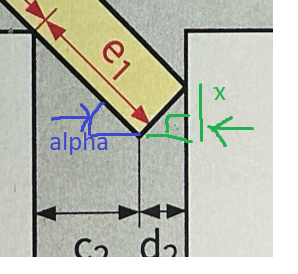
Beispiel: zeichne eine waagerechte Linie ein, die durch die untere Ecke geht. Das ergibt zwei rechtwinklige Dreiecke auf der Straße, in jeder davon findest du α wieder Da die Breite des Teils mit 2,8m gegeben ist, kannst du d2 sofort ausrechnen (abhängig vo α). da die Straßenbreite bekannt ist, kannst du c2 berechnen, und darüber dann e1…
Als Vorüberlegung solltest du so viele Dreiecke wie möglich finden und schauen, was du über die weißt, und wie du sie berechnen kannst. Am Ende wirst du sehen, wie du die tatsächlich benötigte Größe damit ausdrücken kannst.