Hallo zusammen
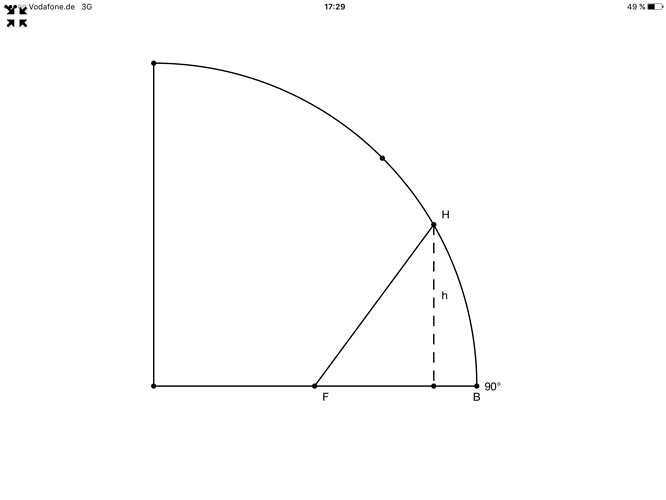
wer kann mir die Fläche FBH des Teilkreises berechnen??
mit der Streckelänge MB = 2
( M ist Mittelpunkt des Vietelkreises: M ist hier nicht angezeigt)
Streckelänge FB = 1 und der senkrechtstehenden Hilfslinie
h = 1
es würde mich freuen, wenn es Hilfe gibt.
mfg
Ralf
Hi.
Du kannst zuerst den Winkel α zwischen MB und MH bestimmen, denn h = Radius * sin(α) .
Die Fläche des „Tortenstücks“ MBH verhält sich zur gesamten Kreisfläche wie α zu 2π.
Davon abzuziehen ist zum Schluß die Fläche des Dreiecks MFH mit Grundlinie MF und Höhe h.
Gruß,
KHK
Vielleicht noch eine Konstruktion in GeoGebra
Nr. Name Beschreibung | Wert
1 Punkt M| M = (0, 0)
2 Punkt F| F = (1, 0)
3 Punkt B| B = (2, 0)
4 Kreis c Kreis mit Mittelpunkt M und Radius x(B)|c: x² + y² = 4
5 Punkt C=(sqrt(x(B)² - 1), 1)|C = (1.73, 1)
6 Sektor s Kreissektor[M, B, C]|s = 1.05
7 Dreieck d Polygon M, F, C|d = 0.5
Die Fläche wäre dann s - d
pda
Hallo keinesherrenknecht
Cooler Name
Die Berechnung der Fläche des Dreiecks MFH über die grundseite MF mit der Höhe h ist genial und einfach.
Bin ich nicht drauf gekommen.
Habe den umständlicheren weg genommen über grundseite MH = r und dazu die Höhe berechnet . Und zwar die Höhe von F auf die grundseite MH. Die kann man ja über den sin Alpha = 30 grad.
Kann man alles machen, aber dein Weg ist cooler.
LG
Ralf