Hallo,
ich suche eine Formel für monatliche Zinseszinsrechnung.
Ich habe manuell eine Beispielberechnung erstellt:
Betrag: 100.000,00 EUR
Zinssatz: 5,00 %
Endkapital in 3 Monaten: 101.255,22 EUR
Dieses Ergebnis müsste also diese Formel wiedergeben.
Danke für Eure Hilfe.
1 Like
Das geht mit der üblichen Zinseszinsformel. Der Zinssatz p ist 5% /12, also 0,004167,
n ist dann die Anzahl der Monate.
Nur um es ganz richtig zu verstehen:
Man tut so, als ob es eine festen Monatszins geben würde und das Geld monatlich mit den Zinsen des Vormonats wieder neu angelegt wird? Das nennt man dann einen „unterjährigen Zinseszins“ und ist absolut vom „üblichen Monatszins“ zu unterscheiden!
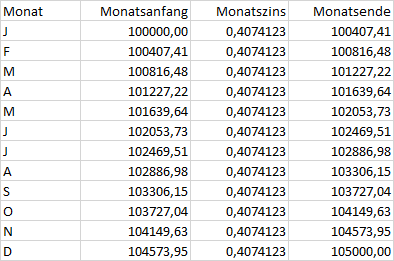
Du kommst dann auf 5% jährlich, wenn du monatlich 0,4074124% Zinsen bekommst und du den Betrag monatlich wieder, zusammen mit dem Monatszins, wieder anlegst.
Und dann stimmt deine Rechnung nicht. Statt dessen würde die Tabelle eines Jahres dann so aussehen:
Lass uns mal warten - gefragt wurde ausdrücklich nach Zinseszins, monatlich. Vielleicht ein Versehen?
Dein Ergebnis (nach 3 Monaten) kommt tatsächlich raus, wenn man mit 5% Zinsen und 0,25 Jahren rechnet. Mit 5%/12 und 3 Monaten kommt das in der Frage angegebene Ergebnis raus. Da scheint es Rundungsdifferenzen bei der Exponentialfunktion zu geben.
Ach so,
wie man auf den Monatszins bei unterjährigem Zinnseszins kommt?
Man nimmt bei 12 Verzinsungsperioden im Jahr einfach die 12. Wurzel aus(1+p/100), also hier von 1,05.
Das Ergbnis ist dann der Faktor, um den sich das Kapital monatlich vermehrt. Hier ist das 1,004074124
Der Monatszins ist dann dieser Faktor, davon 1 abziehen und dann mit 100 multiplizieren. Hier dann 0,4074124%.
Nein.
Es kommt darauf an, ob ich von einer unterjährigen Zinseszinsrechnung ausgehe, oder von einem Jahreszins, den ich gleichmäßig auf die Monate verteile.
Es sind zwei völlig unterschiedliche Berechnungsarten / Vertragsarten.
Man kann durchaus eine monatliche Abrechnung durchführen. Dann gebe ich z.B. für jeden Monat 1% Zinsen.
Am Monatsende schreibe ich diese 1% gut, die Zinsen werden wieder angelegt und im nächsten Monat muss ich das nun um 1% erhöhte Kapital als Basis annehmen.
Man würde so, bei dieser (ungewöhnlichen!) unterjährigen Zinseszinsrechnung bei 1% pro Monat am Ende eines Jahres 12,68% (Zinses-)Zinsen bekommen haben.
Unterjähriger Zinseszins:
https://www.zinsen-berechnen.de/zinsformeln/unterjaehriger-zinseszins.php
Normaler Monatszins:
https://www.zinsen-berechnen.de/zinsformeln/monatszinsformel.php
1 Like
Hallo!
Klar, du kannst den monatlichen Zins ausrechnen, damit inklusive Zinseszins am Ende die 5% raus kommen.
Aber das entspricht nicht der Realität. Tatsächlich gibt es bei monatlicher Zinsauszahlung jeweils 5%/12, wodurch man am Ende des Jahres dadurch tatsächlich 5,12% mehr hat.
1 Like
Der Witz ist doch gerade, dass unterjährige Zinseszinsen zu einem exponentiellen Anstieg des Kapitals im Laufe des Jahres führt,
während die von dir benutzte, normale Monatszinsrechnung absolut linear ist.
Keiner von uns beiden hat Recht oder Unrecht, solange die Frage nicht präzisiert wird.
Du gehst vom banküblichen Fall aus,
ich nehme den Begriff „monatlicher Zinseszins“ wörtlich.
Ich gehe davon aus, dass der Fragesteller den üblichen, also von dir richtig gelösten Fall meint.
Er schrieb aber anders, er möge sich bitte äußern.
Es entspricht sicher nicht der banküblichen Realität,
aber es entspricht der (evtl. irrtümlich falsch) gestellten Frage nach „monatlichem Zinseszins“.
OK, das mit dem Rundungsfehler nehme ich zurück, es sind in der Tat zwei verschiedene Sichtweisen.
Die gewünschte Formel lautet:
101255,22 = 100000 * (1 + 0,05/12) ^3 … (^3 heißt hier: „hoch 3“)
Durch die monatliche Zinseszinsrechnung ist der Effektivzins größer als 5 % p.a.
Hallo,
vielen Dank an alle Teilnehmer. Es gibt sicher
mehrere Sichweisen.
@LittleArrow hat die Formel, die zu meiner Frage
bzw. meinem Ergebnis passt.
Das ist genau das, was ich gesucht habe.
Dafür ein besonderer Dank.
Viele Grüße.
Bitte schön, gern geschehen.
Danke für Dein großes Lob.