Ihr kennt diese Aufgaben, bei denen ein Fahrzeug mit einer bestimmten Geschwindigkeit losfährt und dann von einem zweiten (mit Verzögerung) mit einer schnelleren Geschwindigkeit verfolgt wird. Es soll dann errechnet werden, wann das zweite Fahrzeug das erste einholt. Gibt es dafür eine allgemeine Formel? Ich habe mal selbst herumprobiert und bin nicht zufrieden mit der Ungenauigkeit, die ich bisher erziele.
Ich kann meinen Ansatz hier noch liefern, falls gewünscht.
Moin,
klar. Was für eine Ungenaiugkeit meinst du denn? Eine konstante Geschwindigkeit ist im s/t-Diagramm eine Gerade mit einer bestimmten Steigung. Die erste, die bei t=0 beginnt ist flacher als die zweite, die bei t=tx beginnt. Bei irgendeinem s treffen sich die beiden Geraden also auch die Fahrzeuge. Die beiden Geradengleichungen an diesen Punkt gleichsetzen und der gesuchten Größe umstellen. Das sollte es gewesen sein.
HTH
J~
Hallo,
habe ich gerade einen Denkfehler oder kann man nicht einfach den Vorsprung durch die Differenz der Geschwindigkeiten teilen?
Gruß
Tobias
In der Tat.
Klar, das kann man einfach mal machen:
va - angegebene Geschwindigkeit des A
vb - die des B
dv - Delta v, die Differenz daraus, also dv = vb - va
dt - Delta t, die Zeitdifferenz / Vorsprung des A
Ich erkläre den erstabfahrenden A zum Bezugssystem.
Der B nähert sich nun mit der Geschwindigkeitsdifferenz dv, er ist zu dem Zeitpunkt des Abfahrens va *dt entfernt.
Der Zeitpunkt des Erreichens ist te = (va * dt) / dv (Strecke des Vorsprungs durch Geschwindigkeitsdifferenz)
Der Ort des Erreichens ist dabei s = te * vb (Zeitpunkt des Erreichens mal Geschwindigkeit des Aufholenden)
Zusammen in einer handlichen Formel:
s = va * dt * vb / ( (vb - va) das kann man schöner schreiben:
s = dt * (va * vb)/(vb - va)
Einfach mal testen. A fährt 100s eher los, mit 10m/s. B folgt mit 15m/s.
s = 100s * 150m²/s² / 5m/s
s = 3000m (Einheiten schnell geprüft: Im Zähler hast du s * m * m * s, im Nenner s * s * m, beim Kürzen bleibt im Zähler der m übrig - eine Strecke - passt)
Mein Ansatz war offensichtlich falsch. Ich hatte mir das Folgende überlegt:
wenn ich den Verfolger mal „Fuchs“ nenne, und den Verfolgten „Hase“, dann wäre der Punkt des Zusammentreffens (Treffpunkt) so ausdrückbar:
[(Treffpunkt - Zeitdifferenz beim Start) * Fuchsgeschwindigkeit] - (Treffpunkt * Hasengeschwindigkeit)= 0
Allerdings ist das Umformen, um zum „Treffpunkt = X“ zu kommen dann recht kompliziert.
Selbst als ich das irgendwie hin kam, war ein Test mit konkreten Zahlen nur annähernd richtig, aber nicht präzise (der Gegentest war, die jeweils zurückgelegte Strecke der beiden individuell zu diesem Zeitpunkt zu errechnen und miteinander zu vergleichen).
Was wäre der Zeitpunkt (nicht der Treffpunkt im Sinne von Entfernung) mit dieser Formel?
Du kannst ja hier
etwas experimentieren - Fuchs und Hase müssen ja nicht unbedingt auf dem gleichen Kurs unterwegs sein ;-)…
Hallo,
Gibt es dafür eine allgemeine Formel?
selbstverständlich. Der Problemtyp Deiner Aufgabe ist „Schnittpunkt zweier in Punkt-Steigungsform gegebener Geraden“. Das gehört zu den Basics der zweidimensionalen euklidischen Geometrie.
Falls Du es selbst versuchen willst: Setze y1 + m1 (x – x1) und y2 + m2 (x – x2) gleich und löse die Gleichung nach x auf. Damit hast Du dann auch Deine Aufgabe gelöst. Du musst nur x als Zeit, y als Streckenkoordinate und m als Geschwindigkeit interpretieren.
Lösung:
x = (m2 x2 – m1 x1 – Δy) / Δm
und
y = (m2 y1 – m1 y2 + m1 m2 Δx) / Δm
sind die Koordinaten des Schnittpunkts.
mit Δx = x2 – x1 und Δy = y2 – y1 und Δm = m2 – m1.
Gruß
Martin
Hallo,
danke. Da ist nun allerdings etwas Jargon (fuer Nicht-Mathematiker) in der Antwort mit dabei, der das Verstaendnis sofort erheblich erschwert: was bedeutet das „Dreieck“ (delta?) z.B. bei Δm?
Wenn es Ihnen / Dir nichts ausmacht, waere ein konkretes Beispiel bitte moeglich? Z.B. der erste faehrt mit 56 km/h los, 22 Minuten spaeter faehrt der zweite mit 70 km/h los, wann (und wo) sind sie gleichauf?
Besten Dank.
Hallo,
was bedeutet das „Dreieck“ (delta?) z.B. bei Δm?
das Zeichen „Δ“ ist der Großbuchstabe Delta des griechischen Alphabets. Man verwendet es (unter anderem) zum Abkürzen von Differenztermen, gerade so, wie ich es hier gemacht habe: Δm ist dasselbe wie m2 – m1, nur kürzer geschrieben. Dadurch werden Formeln mit Differenztermen besser lesbar (und auch schreibbar). Nur um Missverständnisse auszuschließen: „Δm“ oder ähnliches bezeichnet KEIN Produkt einer Größe Δ mit einer Größe m! Es handelt sich lediglich um eine Größe, die mit zwei Buchstaben notiert wird.
Z.B. der erste faehrt mit 56 km/h los, 22 Minuten spaeter faehrt der zweite mit 70 km/h los, wann (und wo) sind sie gleichauf?
Dann ist
t1 = 0 min,
s1 = 0 km,
v1 = 56/60 km/min,
t2 = 22 min,
s2 = 0 km,
v2 = 70/60 km/min.
Die Fahrzeuge überholen sich zum Zeitpunkt (gerechnet ab dem Start des ersten Fahrzeugs)
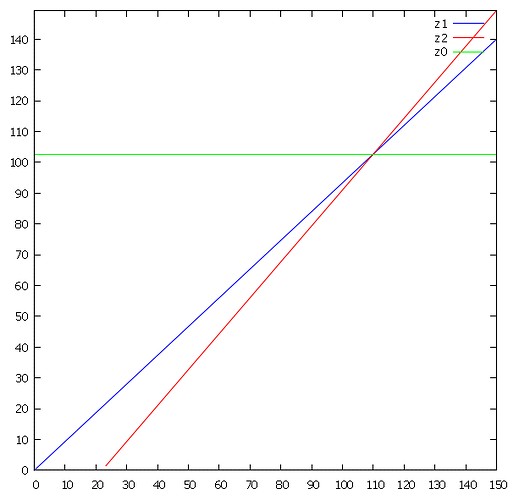
tÜberhol = (v2 t2 – v1 t1 – (s2 – s1)) / (v2 – v1) = 110 min
und das geschieht an der Wegmarke
sÜberhol = (v2 s1 – v1 s2 + v1 v2 (t2 – t1)) / (v2 – v1) = 102.666666 km
Zu beachten ist hier, dass man entweder die Geschwindigkeiten von der Einheit km/h in die Einheit km/min umrechnen muss, oder alternativ die 22 Minuten von der Einheit min in die Einheit h (22 min = 0.3666 h) – sonst liefern die Formeln keine sinnvollen Ergebnisse.
Hier ein Plot des Vorgangs (auf der waagerechten Achse Zeit in min, auf der senkrechten Weg in km):
Gruß
Martin
Super!
Besten Dank, das ist enorm hilfreich und interessant!
Danke nochmals.