Bestimmen Sie, wenn möglich, die Grenzwerte der Folgen
lim
n–>oo
-(1)^n * ((2-n)*(n+3)/(n^2-1)
lim
n–>oo
-(1)^n * ((2-n)*(n+3)/(n^3-1)
kann es sein dass bei beiden der Grenzwert gegen -1 geht
Ok, hab ich. Und jetzt?
In beiden Ausdrücken ist übrigens ein Klammerfehler.
Nein.
Wie sieht denn Deine Rechnung aus, und wo ist das Problem?
hab es probiert über eine Wertetabelle zumachen aber das scheint falsch zu sein
Hallo,
man sollte selbstverständlich die Rechenregeln für Grenzwerte anwenden. Das ist in dem Fall gar nicht so schwierig. Wir haben bei der ersten Aufgabe
ein Produkt aus
-(1)n
und
((2-n)*(n+3))/(n2-1).
Nach den Rechenregeln für Grenzwerte bestimmen wir die Grenzwerte der beiden Faktoren und dann deren Produkt.
Grenzwert für n -> unendlich von -(1)n = ?
Grenzwert für n -> unendlich von ((2-n)*(n+3))/(n2-1) = ?
Der erste Grenzwert sollte klar sein.
Zum zweiten Grenzwert:
((2-n)*(n+3))/(n2-1) ist eine gebrochenrationale Funktion.
a) Echt gebrochenrationale Funktionen (das Polynom im Nenner hat einen höheren Grad als das im Zähler) haben immer den Grenzwert ?, weil der Nenner schneller wächst als der Zähler. Was ? ist, sollte klar sein.
b) Bei unecht gebrochenrationalen Funktionen müssen wir erst eine Polynomdivision durchführen und erhalten dadurch eine ganzrationale Funktion und eine echt gebrochenrationale Funktion als Rest. Dadurch können wir den Grenzwert der unecht gebrochenrationalen Funktion bestimmen, denn der Rest, also die echt gebrochenrationale Funktion hat ja den Grenzwert ? im Unendlichen (siehe oben).
Zum Schluß werden beide Grenzwerte miteinander multipliziert.
Zur Kontrolle die Wertetabelle als Grafik im Intervall [1,1 bis 20]:
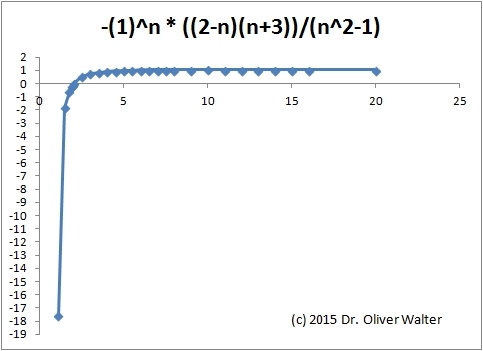
Das gleiche Verfahren wenden wir bei der zweiten Aufgabe an.
Beste Grüße
Oliver
Bitte prüfe die Terme, die Du angegeben hast
meinst Du tatsächlich
-(1)^n oder doch (-1)^n ?
Im Ausdruck ((2-n)*(n+3)/(n^3-1) fehlt eine schließende Klammer. Es ist zwarunwahrscheinlich, aber möglich, dass sie die Interpretation des Terms „auf den ersten Blick“ verändert.
Des weiteren ist die Frage, welches mathematische Handwerkszeug Dir zur Verfügung steht. Schule? Ausbildung? Uni?
Beides könnte nur etwas am Ergebnis ändern, nicht aber an dem von mir beschriebenen Lösungsweg. Die vermeintlich fehlende Klammer könnte auch nur an einer Stelle zu einer Ergebnisänderung führen (bei Setzen nach n3). In den anderen möglichen Fällen schützt das Assoziativgesetz der Multiplikation vor einer Ergebnisänderung.
Außerdem ist nicht gesagt, daß eine Klammer fehlt. Die erste Klammer der gebrochenrationalen Funktion kann als überflüssig angesehen werden und fälschlich gesetzt worden sein.
Beste Grüße
Oliver