Hallo Leute, bin schon wieder am Mathe üben und überlege schon geraume Zeit an der Aufgabe:
In welchen Punkten hat der Graph von f(x) = cos(x) die Steigung m = 1 wenn gilt x größer als aber kleiner als 2 Pie?
Ich habe, wie im Buch hinten auch steht
F(x) = cos(x) abgeleitet also f’(x) = -sin(x)
Danach habe ich 1= -sin(x) gesetzt, nun weiß ich aber nicht wie ich jetzt x ausrechnen soll…
In meinem Buch steht nur, dass die einzige Lösung x= Pie halbe ist…
Nachtrag: Würde mich sehr freuen wenn mir jemand sagen könnte, wie man x ausrechnet
Liebe Grüße
Hallo,
wenn du mit Ableitungen der Kreisfunktionen arbeiten kannst, dann solltest du doch die Kurvenform „in etwa“ kennen.
1 = -sin(x) ist dein Problem?
Forme durch multiplizieren mit -1 um in:
sin(x) = -1
Und nun überlege, wann die Sinuskurve -1 erreicht.
Genau, bei 3/2π
Die "einzige richtige Lösung x=π/2 ist unmittelbar erkennbar FALSCH.
Bei π/2 hat die Cosinus-Funktion eine negative Steigung, sie fällt dort.
erst einaml vielen vielen dank, ich habe gerade gesehen, dass ich mich in der Aufgabe verschrieben habe, ich meinte eigentlich m= -1 somit -1 = -sin(x)
wie bekomme ich hier x raus
also mir ist klar, dass man auch schreiben kann 1 = sin(x)
aber wie kriege ich das x jetzt raus? ich meine rechnerisch
Mir ist bewusst, dass die Sinuskurve 1 im Punkt Pie halbe erreicht.
Also gibt die 1 den y-achenabschnitt an oder?
Eine kurze Anmerkung: π wird „Pi“ genannt und nicht „Pie“, es ist ein griechischer Buchstabe und kein englisches Gericht.
Und sag nicht, du hättest dich vertippt, so oft kann man sich gar nicht vertippen …
Dein Problem ist allerdings, du stellst fragen, wir beantworten sie brav, aber verstanden, was wir da machen, hast du dadurch immer noch nicht (siehe auch andere Aufgabe von gestern).
Sachma, worauf lernst Du denn? Deinen Fragen nach scheinst Du entweder hier Traffic generieren zu wollen oder ein echtes Mathe-Problem zu haben. Ersteres ist natürlich nur eine bösartige, hinterlistige und gemeine Unterstellung darum gehe ich von zweiterem aus. Und da kann ein Forum - wie Christa ja schon schrieb - nicht wirklich helfen. Gibt’s denn keine Nachhilfe, die Dich Deinem mathematischen Ziel (was auch immer es sein mag) näher bringen mag? Älterer Schüler? Tutor? Nachhilfeinstitut?
Okay das mit Pi habe ich einfach falsch geschrieben, aber das mit gestern habe ich wirklich verstanden und das von heute eigentlich auch durch die Antwort von X-Strom
Und blöd bin ich wirklich nicht, wir haben das in der Schule nämlich noch nicht behandelt, ich versuche in den Schulferien nur etwas vorzulernen, weil wir die Bücher in meiner Schule schon fürs nächste Schuljahr bekommen haben
das von gestern schon aber das mit Kreisfunktionen noch nicht
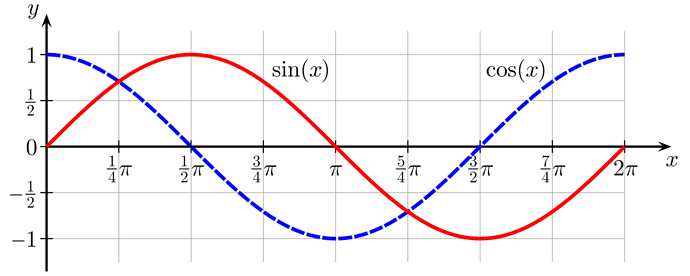
Die Sinusfunktion ist nicht direkt auszurechnen.
Man müsste endlose Berechnungen (Taylorreihen) durchführen.
In der Mathematik ist es daher hier zulässig, den Taschenrechner zu benutzen (oder früher: Tabellenbuch, Rechenschieber).
Da die Umkehrfunktion des Sinus, der Arcussinus, stets Ergebnisse zwischen -π/2 und π/2 liefert (so ist diese definiert!), das Ergebnis von arcsin(-1) aber leider -π/2 liefert und somit außerhalb der gegebenen Lösungsmenge liegt, wäre eine Lösung in etwa so richtig:
sin(x) = 1 ->
x = arcsin(1) + z * 2π (mit z aus Z, Menge der ganzen Zahlen. Das ergibt sich daraus, dass die Sinusfunktion periodisch ist. Wenn sin(x) = y ist, dann gilt das auch für x+2π, x+5π, x-126π, …
Dies ergibt:
x = -π/2 + z * 2π (Die Lösung ist Minus pi Halbe, plus ein ganzzahliges (auch negatives!) Vielfaches von π)
Die Lösungsmenge ist auf Zahlen zwischen 0 und 2π beschränkt, es ergibt sich die Zusatzbedingung
0 <= x <= 2π
Lösung für x einsetzen:
0 <= -π/2 + z * 2π <= 2π | durch π teilen
0 <= - 0,5 + 2 * z <= 2 |durch 2 teilen
0 <= -0,25 + z <= 1 | 0,25 addieren
0,25 <= z <= 1,25
—> Mit z aus den Ganzen Zahlen ist diese Ungleichung nur für z = 1 erfüllt.
Einsetzen in x = -π/2 + z * 2π
x = -π/2 + 2π
x = 3/2 π
