Hallo zusammen,
wir wohnen neben einem Spielplatz. Neulich habe ich einen Jungen von ca. 8-10 Jahren beim Schaukeln beobachtet. Er hat schon in beiden Richtungen fast die Waagerechte erreicht. Könnte er sich mit eigener Kraft mit dem Schaukel überschlagen?
Gruß
Starre Verbindung oder Seil/Kette?
Bei erstem, wenn die Konstruktion keinen Anschlag hat: geht.
Bei einer losen Aufhängung vermutlich eher nicht. Man müsste die Energie für die letzten 90° ja irgendwie in einem Schwung aufbringen. Damit man zumindest von oben auf den Querbalken knallt.
grüße
lipi
Hallo,
ergänzend zu den Ausführungen von @littlepinguin: bei Myth Busters hat man mal versucht, Überschläge auf Ketten-Schaukeln zu erreichen.
Es funktionierte.
Also erst beim letzten Versuch, der auf die, für diese Sendung sehr typische, hochexplosive Weise durchgeführt wurde. Man setzte einen Dummy in die Schaukel, befestigte Raketenantriebe am Sitz und beschleunigte den Dummy auf diese Weise so stark, dass er mehrere Überschläge schaffte.
Ansonsten, wie schon geschrieben: mit einer Kettenschaukel kann es nicht funktionieren. Mit einer Schaukel mit einer starren Aufhängung des Sitzes dagegen problemlos.
Grüße
Pierre
Moin,
warummenich, warummenich? Höchst interessante Fragestellung. Meine Vermutung: Sobald die Schaukel über den Aufhängepunkt kommt, fällt die Schaukel senkrecht, bis die Kette wieder gestrafft ist und kann in der Zeit nichts zum Drehmoment beitragen. Fragt sich natürlich, wo die Energie bleibt. Nächste Vermutung: die Bremsenergie fürs Kettenstraffen, genauer: für die Richtungsänderung von der Senkrechten in die Kreisbahn, fließt als Wärme in Gerüst und Kette.
Gruß
Ralf
Mei Jung, ich werd Dir das mal vertellen.
Die Probleme beginnen bereits an bei beiden 90° Punkten der gewollten Kreisbewegung (wobei in meiner Betrachtung 0° senkrecht hängend sei). Um so hoch zu kommen, beschleunige ich ja die Schaukel gegen die Gravitation und durch die Verbindung mit dem Kreismittelpunkt (die Querstange) erreiche ich ein Drehmoment. Nun habe ich als Mensch mit meiner Bewegung nur eine begrenzte Kraft, die Gravitation ist rocht recht stark. Ich komme nur bis zu einem gewissen Punkt, dann obsiegt sie. Allerdings kann ich ihre Wirkung mitnehmen und beim Schaukeln in die andere Richtung wieder etwas Energie oben drauf tun, wodurch die Amplitude bei jedem Schaukeln ein wenig größer wird. Bis zum 90° Punkt. Wenn ich darüber komme, wandelt die Gravitation die Bewegung nicht mehr in eine Rotation, sondern erst mal in einen linearen Fall. Die Rotationsenergie, die ich für den nächsten Schwung mitnehmen kann, verringert sich dadurch. Irgendwann wird es entweder zum Nullsummenspiel mit viel Ruck. Oder ich komme tatsächlich schon so hoch, dass ich mich an der Stange verletzen kann.
Lediglich, wenn ich sehr viel Kraft aufbringe, im Experiment mit den Raketen, ist das Drehmoment so groß, dass es praktisch keinen Totpunkt mehr gibt, an dem ich fallen könnte.
Da ich im Physikunterricht nicht zu jeder Stunde zu 100% anwesend war (die Restaufmerksamkeit reichte, um durchgehend Einsen zu schreiben), bekomme ich Begriffe wie kinetische oder potentielle Energie leider nicht mehr so ganz auf die Reihe. Zudem habe ich sie in den Jahrzehnten seit meinem Abschluss auch zu selten (praktisch nie) benötigt. Ich lasse mir also in diesem Punkt gerne auf die Sprünge helfen.
Hi,
ich gehe davon aus, dass in Deutschland, wo so ziemlich alles reglementiert ist, auch daran:
gedacht wurde und vermutlich konstruktionsbedingt genau das verhindert wird.
Ich habe die Frage auf den konkreten Fall und nicht auf eine theoretische Schaukel bezogen. 
Gruß
Christa
Och Pierre, das ist doch in Höhe der Aufhängung. Aber iss wurscht, wir meinen wohl das Gleiche.
Noch 'n Versuch: Kinetisch habe ich, potentiell könnte ich. Odrr?
Gruß
Ralf
hi,
das wäre ja abartig dämlich, weil der Anschlag (wenn man ihn nicht explizit wegkonstruiert, wäre das der Balken selbst) schlimmeres verhindert.
Seile und Ketten verringern die Gefahr imo aber generell.
Auch wenn sie ‚außer Kontrolle‘ sind, hat so ne starre Schaukel etwas mehr bums.
grüße
lipi
Servus, Christa,
ein Anschlag würde die Unfallgefahr keineswegs mindern. Ich vermute (schon wieder, soifz), dass deshalb die Überschlagschaukel mit den Stangen nur auf dem Jahrmarkt erlaubt ist, ansonsten gibt es nur Kettenschaukeln. Ächz - issjaganichwah, in jedem Garten stehen die Dinger mit dem Autoreifen oder der Liegeschale rum. Keine Ahnung, ob da ein Anschlag dran ist.
Gruß
Ralf
Ich weiß nicht, ob wir uns richtig verstanden haben, ich glaube eher nicht. Ich meinte, dass konstruktionsbedingt der Anschlag vorhanden ist und dadurch ein Überschlag verhindert wird. 
hi,
ok. falsch verstanden.
Dann war es der gleiche Gedanke, daher die Einschränkung, dass eben kein Anschlag vorhanden sein darf.
grüße
lipi

Nanu! Kinetisch - ich bewege mich, potentiell - ich könnte mich bewegen. Allns kloar?
Auf den heutigen Spielplätzen (in Deutschland) wohl eher nicht mehr. Zumindest gibt bzw. gab es Überschlag-Schaukeln:
Zudem ist es eine estnische Sportart: https://de.wikipedia.org/wiki/Kiiking
Nicht ganz. Die Kette wird durch die auf sie wirkenden Kräfte gespannt, das sind Gravitation und Fliekraft. Die Fliehkraft wirkt dabei immer „spannend“, hängt aber von der Geschwindigkeit ab.
Die Gravitation wirkt immer nach unten, der Anteil entlang der Kette wirkt daher unterhalb von 90° spannend, darüber jedoch dem entgegen.
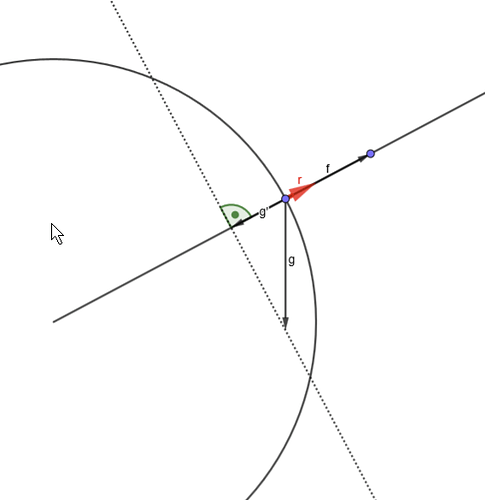
Im Bild geht es grade noch gut, die Fliehkraft f ist stärker als der parallel zur Kette wirkende Anteil g’ der Gravitation, die resultierende Kraft r wirkt nach außen:
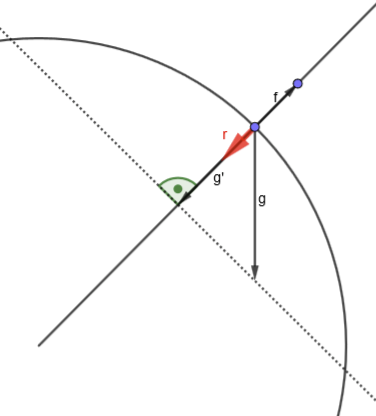
Etwas höher, und die Fliehkraft ist durch die nun geringere Geschwindigkeit ebenfalls kleiner. Duch die verschobenen Winkelverhältnisse wirkt der Anteil g’ der Gravitation nun stärker, und die Resultierende zeigt nun zur Achse hin - die Kette wird nicht mehr gespannt:
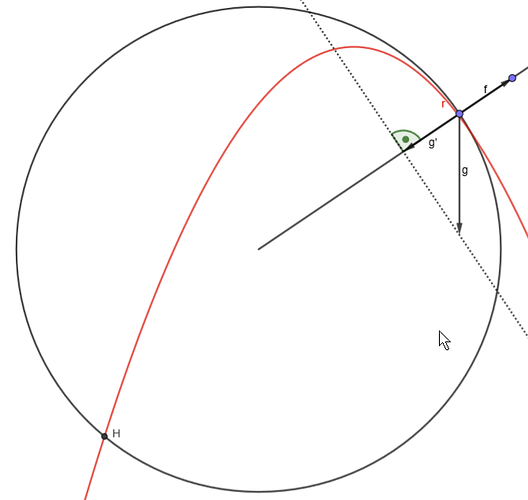
Das Problem tritt in dem Moment auf, in dem sich f und g’ genau aufheben, die Resultierende r also 0 ist. Die Kette ist nicht mehr gespannt, die schaukelnde Person unterliegt nur noch der Gravitation. Da die Person sich aber immernoch nach links oben bewegt, fliegt sie nun eine Wurfparabel, bis sie links unten bei H ankommt. Der Punkt liegt sehr tief, die Person hat daher fast Maximalgeschwindigkeit, und weil sie fast parallel zur Kette dort ankommt, wird sie äußerst unsanft gestoppt.
Solange das ganze knapp über 90° passiert, ist das noch kein Thema, die Person fällt da annähernd senkrecht, und wird von der Kette wieder sanft aufgefangen. Aber irgendwann wird’s ungemütlich.
Und: hat die Schaukel statt einer Kette eine starre Verbindung, gilt für die Kräfte prinzipiell das gleiche - die Schaukel selbst wird aber auf die Kreisbahn gezwungen - die Person wird allerdings durch die Resultierende r aus ihrem Sitz gehoben, muss sich also gut festhalten, oder besser angeschnallt sein.
Ach ja… wo die Energie bleibt…
Das hängt davon ab, wie man das ganze modelliert. Vollelastisch betrachtet spannt sich die Kette wie eine Feder und zieht die Person wieder zurück, so, als würde da ein Flummi bei h auftreffen. Die Bewegungsenergie wäre dann vollständig erhalten.
Total unelastisch betrachtet wird die Person mit einem Ruck bei H gestoppt und bewegt sich nur noch mit der (kleinen) Geschwindigkeitskomponente parallel zur Kreisbahn weiter, als würde dort ein Sandsack aufprallen.
Die dabei „verschwindende“ Energie geht in Verformung und Wärme über.
In der Realität hat man eine Mischung aus beidem, die Person ist allerdings mehr Sandsack als starrer Körper. Denkbar ist auch, dass die Kette reißt.
Oh, und noch was: Die Person bewegt sich beim Schaukeln ja nicht nur auf ner Kreisbahn, sie selbst dreht dich dabei ja auch um sich selbst. Während sie also auf der Parabel fliegt, dreht sie sich auch weiter. Möglicherweise trifft sie bei H mit dem Kopf nach unten auf, und macht Bekanntschaft mit dem Boden.
Servus, Christa,
kurze Recherche hat ergeben: Die Garten- und Spielplatzschaukeln haben keine Stangen, sondern Ketten. Damit braucht es keinen Anschlag, es geht eh nicht.
Abgesehen davon vermute (schon wieder!) ich, dass bei Stangen eine gewisse Mindesthöhe nötig ist, um die Schaukel überhaupt hoch genug zu bekommen. Der „Höhengewinn“ erfolgt ja dadurch, dass der Sportler sich beim Fallen streckt, um seinen Schwerpunkt so hoch wie möglich zu kriegen, und beim Steigen in die Hocke geht, auf dass der Schwerpunkt möglichst tief liege. Das ist das gleiche Prinzip wie beim Fosbury-FLop, bei dem ja bekanntlich der Schwerpunkt unter der Stange bleibt.
(Was der Sportler anstellen muss, um nach Überschreiten des Scheitelpunktes den Schwerpunkt wieder nach oben zu kriegen, mag ich mir jetzt nicht ausmalen, er steht ja immerhin auf dem Kopf resp. hängt an den Füßen.)
Falls das Gestänge recht kurz wäre, etwa unter 2 m, kann mE während des Fallens nicht genug Fahrt aufgenommen werden, um in einen Überschlag zu münden. Jetzt wäre halt schön, wenn das jemand nachrechnen könnte, dazu reicht es bei mir leider nicht (mehr).
Gruß
Ralf
ps: beim Fosbury-Flop geht der Springer natürlich nicht über die Stange, sondern über die Latte.
Hi!
Mit jeder Schwingung kann man etwas mehr Energie rein stecken, das gilt auch in einer Schaukel mit Stangen. Und irgendwann ist der Punkt erreicht, wo es für einen Überschlag reicht. Bis dahin muss man sich aber gut festhalten.
Das Prinzip ist immer dasselbe: Am höchsten Punkt geht man in die Hocke und am tiefsten Punkt streckt man sich durch. Das wird um so effektiver, je größer der Winkel am höchsten Punkt ist. Ab einem Winkel von 90° wird sogar in beiden Fällen Energie ins System gepumpt. Dadurch könnte eine kleine Schaukel die Sache sogar vereinfachen, weil man mit der gleichen Energie einen größeren Winkel erreicht. Eine Mindesthöhe gibt es nur, weil man Platz braucht, um sich aufzurichten.