P2 liegt ja konstruktionsbedingt auf AS2.
Und AS2B sowie AS2P1 sind Nebenwinkel. Letztgenannter dann auch 90 Grad über P1P2.
Deine Argumentation durchdenke ich noch.
Bis später
Catrin
Nachtrag: Ich habe die Aufgabenstellung nochmal gründlich gelesen und festgestellt, dass genau ausgeschlossen ist, dass AS1 den Kreis 2 in S1 und AS2 den Kreis 2 in S2 schneiden darf. Damit darf der Beweis auf die Weise mit den Tangentenabschnitten nicht geführt werden. Es ärgert mich, dass ich das überlesen habe.
Alles klar. Sorry. Ich hatte A auf der anderen Seite der Geraden M1M2 liegen. Dann tauschen P1 und P2 ja ihre Plötze.
Dann stimmt deine Argumentation natürlich. Aber sie setzt etwas voraus: Daß AS1 und BS2 sich in P1 schneiden. Dann aber schneiden sich AS2 und BS1 auch in P2. Nämlich diametral gegenüberligende Punkt A und B auf Kreis1 erzeugen dieselben Schnittpunkte auf Kreis2.
Dann ist aber nicht nur AS2P1 ein rechter Winkel, sondern auch AS1P2. Denn auch S1 liegt auf dem Thaleskreis über AB. Somit liegen sowohl S2 als auch S1 auf Thaleskreisen über P1P2.
Da P1P2 dann auf einem Durvchmesser liegt, liegen die Schnittpunkte, die umgekehrt P1S1 und P1S2 auf Kreis1 erzeuigen, ja ebenfalls auf einem Durchmesser, nömich AB.
Übrigens liegen die Durchmesser-Geraden AB und P1P2 auch orthogonal zueinander.. Auch das natürlich nur bei orthogonalen Kreispaaren.
Danke, es ist wirklich ein schöner komplexer Sachverhalt. Ich werde rückspiegeln, wie die Lösung reflektiert wurde.
Bis dahin viele Grüße
Catrin
So ist es, eine erstaunliche geometrische Struktur. Deshalb hab ich mich auch etwas intensiver reingehängt. Habe es einmal umgekehrt konstruiert: Angefangen mit P1, P2 auf einem beliebigen Kreis …
Hier die Graphik dazu, mit verschiebbaren Punkten:
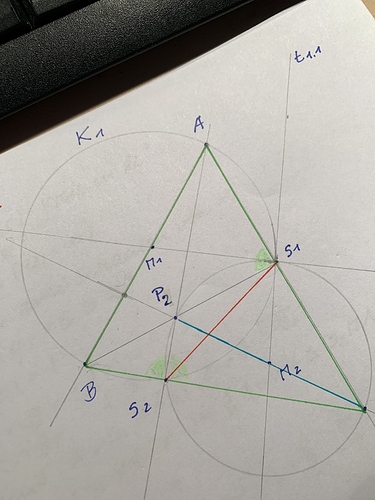
(1) schwarz: Kreis1 „k1“ mit Mittelpunkt M1 und darauf 4 beliebige Punkte P1, P2, S1, S2
(2) rot: Zwei Geraden P1S1 und P2S2 schneiden sich in einem Punkt A
(3) rot: Zwei Geraden P1S2 und P2S1 schneiden sich in einem Punkt B
(4) blau: Ein 3-Punkte-Kreis „k2a“ S1S2A mit Mittelpunkt M2a
(5) blau: Ein 3-Punkte-Kresi „k2b“ S1S2B mit Mittelpunkt M2b
(6) grün: Tangenten an k2a in S1, S2
Legende:
Punkte P1, P2, S1, S2 auf k1 verschieben: Mit Maus (linke Taste) den Punkt „anfassen“
Graphik vergrößern mit Mausrad
Graphik verschieben: linke Maustaste irgendwo auf freiem Platz
(7) Die Mittelpunkte M1, M2a, M2b sind immer kolinear
(8) die Kreise k2a und k2b sind allgemein ungleich groß
Aber wenn du P1, P2 so verschwiebst, daß sie auf einem Durchmesser von K1 liegen, dann:
(9) Die Kreise k2a und k2b sind gleichgroß und koinzident.
(10) Die Tangenten (grün) in S1, S2 an k2a schneiden sich in M1
⇒
(11) Die Kreise k2a und k1 sind orthogonal. q.e.d.
Gruß
Metapher
Danke für dein „Reinhängen“ - find ich toll. Das macht es total übersichtlich in meinem Kopf. Bin gespannt, wie das Feedback auf die Lösung sein wird.
Herzlich
Catrin
Der Beweis an sich ist so durchgegangen. Abzug gab es dafür, dass ich nicht begründet habe, warum P2 auf BS1 und auch AS2 liegt.
Bei uns früher in den Vorlesungen war ein „geflügtes Wort“ unserer Professoren:
„Es ist offensichtlich, dass…“ oder „Man sieht, dass…“ ![]()
Ich habe bei Deinen Aufgaben nur gestaunt, dass ich das früher (vor 40 Jahren) mal alles verstanden hab, man braucht es aber nie wieder…
LG Beatrix
Ja, Beatrix, oder „Wie man leicht sieht …“ ist auch nett ![]()
Es ist für die Lehramtsausbildung sicher über das Ziel hinaus. Aber es macht mir trotzdem Spaß, man lernt vor allem hier im Forum sehr viel mehr dazu, als in der VL:
Herzlich
Catrin
Dieses Thema wurde automatisch 30 Tage nach der letzten Antwort geschlossen. Es sind keine neuen Nachrichten mehr erlaubt.