Hallo Experten Mathe,
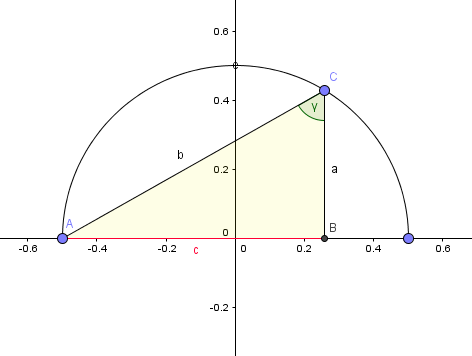
in einem Kreis mit Umfang Pi zeichne man auf dessen horizontalen Durchmesser ein rechtwinkliges Dreieck, dessen Punkte A und C exakt auf dem Kreisbogen liegen (der rechte Wikel liegt in Punkt B; B befindet sich auf dem horizontalen Durchmesser des Kreises rechts von Punkt A, der identisch ist mit dem Schnittpunkt des horizontalen Durchmessers mit dem Kreisbogen auf der linken Seite des Kreises, d. h. Seite c liegt auf diesem Durchmesser; die Strecke CB oder Seite a des Dreiecks ist das Lot von C nach B, also das Lot vom Kreisbogen oberhalb des horizontalen Durchmessers aus bis zum Punkt B). Nun gelten folgende Gesetze: Länge Seite b (Hypotenuse) = cos Alpha (cos als cos mit Längeneinheiten gesehen, nicht nur als Wert betrachtet) sowie b^2 = c. Die Gesetze gelten grundsätzlich, egal wie man das Dreieck in den Kreis zeichnet, vorausgesetzt, die Regeln oben werden eingehalten! Schön und gut, aber wie kann man das beweisen? Hat einer eine Idee? Vielen Dank für alle Bemühungen.
Grüße Thomas
Kurze Ergänzung von mir: Es handelt sich natürlich nicht um den Einheitskreis, sondern um einen Kreis mit Durchmesser = 1
hi,
mach aus deinem Kreis mal einen Halbkreis und versuche die Werte anhand einer Sinuskurve grafisch zu ermitteln.
grüße
lipi
Hallo Thomas,
soll „B“ der Mittelpunkt des Kreises sein?
Woher hast du die Gesetze?
Gruß
Pontius
Abgesehen von deiner unkonventionellen Bezeichnung der Seiten (man nennt normalerweise die Hypothenuse „c“):
Es gilt: rRadius = 1/2 = a = c
Bei den Behauptungen (das sind keine „Gesetze“!)
- cos α = b
und - b2 = c
betrachtest du die Strecken offenbar dimensionslos.
Nun gilt: b ist die Diagonale des Quadrates über c bzw. über a
Also
b = a √2 = c √ 2= 1/2 √2 = 1/√2
Ferner gilt:
cos α = a/b = c/b
Damit solltest du nun
cos α = b
und
b2 = c
leicht verifizieren können.
Gruß
Metapher
B kann der Mittelpunkt sein, aber auch jeder beliebige Punkt auf dem Radius von links bis zur Kreismitte
Sowie jeder beliebige Punkt auf dem horizontalen Durchmesser
Die Gesetze habe ich durch Probieren heraus gefunden
Hi Martin,
gut, also B liege beliebig zwischen (-0,5|0) und (+0,5|0).
Allerdings sollte α bei A(-0,5|0) liegen.
Die Gleichungen stimmen - wie leicht zu sehen - für B(0|0) (s.o.) und auch für B(+0,5|0). Leicht auch zu beweisen. Witzigerweise stimmen sie rein rechnerisch auch für alle Zwischenwerte von Punkt B. Bei dem Beweis dafür steh ich grad noch auf dem Schlauch ![]()
Gruß
Metapher
Nur weil du etwas heraus gefunden zu glaubst, ist es noch kein Gesetz.
Deine Behauptung b^2 =c ist z.B. über den Höhensatz des Euklid beweisbar:
h^2 = p * q
entspricht gem. deinen Bezeichnungen:
a^2 = (1-c) * c = c - c^2
b^2 = a^2 + c^2
für a^2, c-c^2 eingesetzt ergibt:
b^2 = (c - c^2) + c^2
b^2 = c
q.e.d.
Hi @Thomas_Spilles
Rein rechnerisch aus der Zeichnung von @Martin zumindest für die Behauptung b2 = c
r sei Radius = 1/2. M sei Mittelpunkt. Sei c’ die Strecke M ⇆ B
Dann gilt:
c = c’ +1/2
und
c’2 = r2 - a2
Dann ist
c = 1/2 +√ ( r2 -a2)
Ferner
b2 = a2 + c2
b2 = a2 + (1/2 +√ ( r2 -a2))2
Binom ausgerechnet:
b2 = a2 + 1/4 + √ ( r2 -a2) + r2 -a2
Mit r2 =1/4 folgt
b2 = 1/4 + √ ( r2 -a2) + 1/4
b2 = 1/2 + √ ( r2 -a2) = c
q.e.d.
Und weiter aus der Zeichnung:
Betrachtet das Dreieck A - C - A’ mit A’(+1/2|0) (wie bei der Rechnung von @Pontius).
Der Winkel α liegt im Eckpunkt A. Und er ist daher derselbe wie im Dreieck A-C-B.
cos α = Ankathete/Hypothenuse = b/(c+(1-c)) = b/(c+1-c) = b
q.e.d.
Meine Behauptungen gehen noch weiter: für beliebige Kreise gilt nämlich
- b = D * cos Alpha sowie
- b^2 = D * c
Bitte korrigieren, falls ich falsch liege!
Übrigens vielen, vielen Dank für die große Hilfe von Euch!!!
bzw. Eure Hilfe (korrektes Deutsch)
Das ist trivial, weil doch D = 1
Im Übrigen ist (siehe unten)
cos α = b/D = Ankathete/Hypothenuse gerade die (geometrische) Def. des Cos.
Korrektur:
„Nur weil du glaubst, etwas heraus gefunden zu haben, ist es noch kein Gesetz.“
Hallo,
Satz des Pythagoras im Doppelpack – einmal für das Dreieck ∆ABC und einmal für das Dreieck ∆0BC hinschreiben:
c2 + a2 = b2
(c – r)2 + a2 = r2
Nach Auflösen der Klammer und anschließender Vereinfachung sieht die zweite Gleichung so aus:
c2 + a2 = 2rc
Nun steht auf der linken Seite laut der ersten Gleichung gerade b2 und damit ist man auch schon fertig:
b2 = 2rc
Der Kosinus des Dreieck-Innenwinkels im Punkt C ergibt sich zu
cos(…) = c/b = (b2/2r)/b = b/(2r)
Für r = 1/2 folgen daraus sofort Deine Resultate b2 = c und cos(…) = b.
Gruß
Martin
Bei beliebigen Kreisen ist doch D auch beliebig, also nicht trivial?