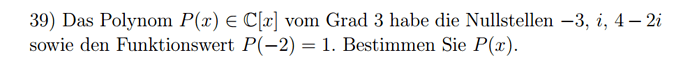Langrange Interpolation + Gleichungsystem lösen + komplexe Zahlen?

[sargan26]

Hallo, ich verzweilfe gerade an folgendem Beispiel:

ich wir lernen gerade über Langrande Interpolation (vllt. hat es damit etwas zu tun obwohl ich ein ähnliches Beispiel nur mit Gaußem Logarithmus lösen konnte).

Mein Ansatz wäre:

Ersten drei Zeilen sind die Nullpunkte -3, i und 4-2i in die allgemeine Formel eingesetzt und die letzte Zeile P(-2)=1. Schaffe es aber nicht mit Gauß aufzulösen

Vielleicht habt Ihr Ideen.
Danke!
Daniel

[sweber]

Hallo!

Du denkst viel zu kompliziert.

Ein Polynom 3. Grades hat immer drei Nullstellen, die bereits gegeben sind. Damit ist es schon bis auf einen konstanten Vorfaktor bekannt:

P(x) = a*(x+3)*(x-i)*(x-4+2i)

und mit der Forderung P(-2)=1 kannst du auch a ausrechnen.

Dafür müßtest du erstmal die drei Klammern ausmultiplizieren, zur Kontrolle hier das Ergebnis:

x³+(-1+i)x²+(-10+7i)x+6+12i

[sargan26]

Bist der Beste!