Hallo,
ich würde gern diese lineare Gleichungssystem mit 6 Gleichungen und 6 Unbekannten mit Gauß Algorithmus lösen. Ist dies überhaupt möglich ohne den Betrag der bekannten Konstanten zu wissen? (z.b. Gleichung 5 steht bei S1 „5 l / E A“ und dies kann ich nicht eliminieren ohne den Wert der Konstanten zu wissen oder?)
Auf der Uni wurde es mit Einsetzen gerechnet (siehe unten) und entsprechend Ergebnis mit den Konstanten hingeschrieben.
Hallo!
Du kannst das durchaus auch mit Gauß rechnen. Beispielsweise kannst du V-(5L/EA)*I rechnen, und bist die erste Komponente von V los. Danach bietet sich sich an, das neue V mit VI zu verrechnen, um die zweite Komponente zu eliminieren, und so weiter. Du benötigst da nur etwas Konzentration, denn die Elemente sind nicht mehr einfache Zahlen, sondern schnell mal etwas unhandliche Terme.
Unangenehm ist aber eine Sache, die du immer berücksichtigen mußt: Was ist, wenn eine Komponente, z.B. 5L/EA gleich null ist? In dem Fall also, wenn L=0 ist?
Dafür braucht es eine Fallunterscheidung. Schreibe das ganze Gleichungssystem nochmal auf ein neues Blatt, und setze für L überall 0 ein. Du bekommst dann ein ziemlich spärlich besetztes Gleichungssystem, das zumindest keine Parameter mehr enthält.
Da dies eher eine physikalische Aufgabe ist, kannst du vermutlich davon ausgehen, daß dich Lösungen für L=0 eh nicht interessieren, und brauchst die Fallunterscheidung nicht zu machen.
Hallo,
Da dies eher eine physikalische Aufgabe ist, kannst du vermutlich davon
ausgehen, daß dich Lösungen für L=0 eh nicht interessieren, und brauchst
die Fallunterscheidung nicht zu machen.
so sehe ich das auch. Dasselbe gilt auch für die Fälle E = 0 und A = 0. Wenn eine dieser Größen Null ist, verlieren bereits die entsprechenden Ausgangsgleichungen ihren Sinn, und damit auch die Frage nach einer Lösung.
Die Länge L ist die natürliche Längeneinheit des Problems und das Produkt EA ist dessen natürliche Krafteinheit. Durch Einführung neuer Variablen
φk := Sk/(αT EA) (k = 1, 2, 3)
und
λk := lk/(αT l)
kann man die Ausgangsgleichungen entdimensionalisieren und wenn man die neuen Gleichungen dann in Matrixnotation darstellt (mit (φ1, φ2, φ3, λ1, λ2, λ3) als Vektor „x“), enthalten sowohl die Koeffizientenmatrix als auch der Konstantenvektor nur noch Zahlen (@TO: probiers mal aus).
Inwiefern es zum Erkenntnisgewinn beitragen soll, dieses Gleichungssystem von Hand zu lösen, erschließt sich mir nicht. Ich denke, heute darf man so etwas getrost einem CAS überlassen.
Gruß
Martin
Das Mechanik Institut quält halt die Studenten gern.
Hab noch ein gutes Erklärvideo gefunden falls es jemand braucht.
Und was dahinter steckt begreift keiner - ist ja aber auch egal, wenn dann mal Mist rauskommt und keiner was merkt.
Tolle Wurst.
Ich kann vor all diesen tollen Automaten nur DRINGEND warnen!
Gruß
damals
Nö. Das legt nur sinnvollerweise Wert darauf, dass die Lernenden wissen, was sie tun. Knöpfchen drücken hat noch nie zu neuen Erkenntnissen geführt, das kann man sich komplett sparen.
Gruß
damals
Hallo,
Und was dahinter steckt begreift keiner
hm – wer hat diese komplexen Systeme dann programmiert? Hälst Du es für möglich, dass es Personen gibt, die über mathematische Fachkenntnisse in einem Umfang verfügen (erworben z. B. im Laufe eines Studiums), welches sie in die Lage versetzt, sogar im Detail zu verstehen, was dahintersteckt? Die mathematischen Verfahren, mit denen ein CAS eine bestimmte Berechnung, etwa eine Gauß-Elimination, durchführt, sind übrigens auch kein Geheimnis, sondern in der Dokumentation genau beschrieben. Mit künstlicher Intelligenz haben Computer-Algebra-Systeme auch nichts zu tun. Von daher kann ich Dein Statement „was dahinter steckt begreift keiner“ nicht nachvollziehen.
ist ja aber auch egal, wenn dann mal Mist rauskommt und keiner was merkt.
Wie groß dieses Risiko ist, hängt sehr vom Typ des Problems ab. Für viele Aufgabenstellungen ist es überschaubar oder sogar gleich Null. Mit einem CAS kann ich mir z. B. auch die Fakultät von 99 oder die dritte x-Ableitung von xn/(x + n) ausrechnen lassen, und warum sollte ich dann den Resultaten nicht vertrauen dürfen? In Zweifelsfällen überprüft man Ergebnisse halt durch Proberechnen. Natürlich gibt es auch Sachen, die für gewisse Fehler anfällig sind (Abbruchfehler, numerische Stabilität etc.); dann ist diese Problematik aber wohlbekannt und man kann sich darauf einstellen. Mit der Frage, wann wo welcher Mist rauskommen und wie man das merken kann, beschäftigt sich die Disziplin der praktischen Mathematik/Numerik sehr intensiv.
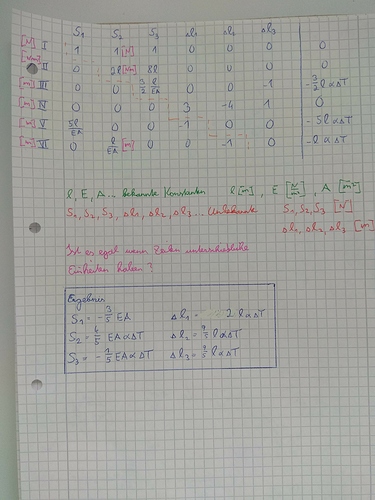
Das Problem des Fragestellers lässt sich erstmal auf dieses lineare Gleichungssystem (LGS) reduzieren (diesen Teil der Arbeit kann kein Automat übernehmen):
(1 1 1 0 0 0 | 0) (0 2 8 0 0 0 | 0) (0 0 0 3 -4 1 | 0) (5 0 0 -1 0 0 | -5) (0 1 0 0 -1 0 | -1) (0 0 3/2 0 0 -1 | -3/2)
Nun guckt man sich das an: Es ist ein dünnbesetztes, quadratisches System der Dimension 6, d. h. es ist ein „kleines“ System. Die Koeffizienten sind alle in derselben Größenordnung. Außerdem weiß man, dass das System eindeutig lösbar sein muss. Wenn das CAS also irgendetwas anderes befinden sollte, d. h. „unlösbar“ oder „mehrdeutig lösbar“ (was man am Output sofort erkennt), dann kann man sich auf die Suche nach dem Grund dafür begeben und den Fehler korrigieren.
Die Lösung ist
(-3/5, 4/5, -1/5, 2, 9/5, 6/5)
und ihre Korrektheit lässt sich mit einer simplen Probe verifizieren. Ich habe wirklich keine Ahnung, welcher Sinn oder Nutzen darin liegen soll, das mit Bleistift und Papier auszurechnen (vorausgesetzt, man könnte es mit Bleistift und Papier ausrechnen). Ich rechne übrigens auch 57164 · 82743 oder 49380/5 nicht von Hand aus, sondern tippe das bedenkenlos in einen „tollen Automat“ (namens Taschenrechner) ein.
Gruß
Martin
Der Name steht leider nicht drunter. Und ich wüsste auch wirklich nicht, was der zum Thema beitragen könnte.
Die liest kein Mensch. Viel zu kompliziert.
Ja. So wie bei der Marsmission, hm? Oder beim Airbus.
Woher sollen denn die Zweifel kommen, wenn man gar nicht weiß, was in der Black Box passiert? Dass und welche Sonderfälle es gibt, in denen das Verfahren nicht funktioniert? Ich habe hier schon einige Studenten erlebt, die sich unter ‚1000W-Widerstand‘ genau gar nichts vorstellen konnten und denen bei einem solchen Ergebnis nicht die leisesten Zweifel gekommen sind.
Dein zu-Fuß-rechnen beweist leider genau gar nichts - außer dass du persönlich weißt, wie’s geht. Das nutzt den Studenten exakt nichts.
… benutzt man heutzutage nicht mehr. Die App heißt ‚Matlab‘.
Gruß
damals
