Könnte mir eventuell jemand zeigen wie man diesen Doppelbruch vereinfacht?
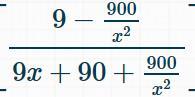
Könnte mir eventuell jemand zeigen wie man diesen Doppelbruch vereinfacht?
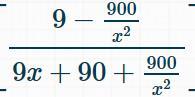
Magst du das vielleicht erstmal probieren und uns hier das Ergebnis deiner Bemühungen schildern? Letztens schriebst du etwas von einer Klausur, es ist dir damit nicht geholfen, wenn du dir das alles von uns berechnen lässt, so etwas lernt man nur durch Üben.
Kleiner Tipp zur Vorgehensweise: ich würde Zähler und Nenner jeweils auf den gleichen Nenner (x2) bringen, dann den Nenner wegkürzen, anschließend kannst du im Zähler und im Nenner die 9 ausklammern und ebenfalls wegkürzen.
Wenn ich auf vernünftige Ergebnisse kommen würde hätte ich doch ganz sicher hier nicht gefragt. ![]()
Außerdem darf ich mir einen 10 Seitigen Spickzettel mitnehmen auf dem ich mir die Rechenwege aufschreiben kann. Damit es wegen so Kleinigkeiten nicht hackt. -.-
Den Rechenweg habe ich beschrieben, rechnen kannst du selbst, oder weißt du nicht mal, wie man Brüche auf den gemeinsamen Nenner bringt? Reden wir hier von Sekundarstufe I oder vom Studium??
Aber der Fragesteller gehört ja wohl verhauen. Sooo schöne dritte binomische im Zähler - und dann kann man NIX damit anfangen grmpf
Hallo,
auf den ersten Blick zu sehen: Die 9 ist wegkürzbar.
Gruß
Martin
Das ist nicht das Problem. Aber du läßt halt so gar keine Eigeninitiative erkennen. Da zu helfen macht nicht wirklich Spaß ![]()
Ich glaub es hakt (sic!).
Was ist das denn für ne komische Klausur, in der ein 10 (!) seitiger Spickzettel erlaubt ist? Mathe im „Sozialen Zweig“? - Ach nee, du machst ja was mit Wirtschaftsmathematik…
Aber sei’s drum: Was schreibstn da rein, in deine Spickbroschüre? Alle möglichen Doppelbrüche?
„So Kleinigkeiten“ wie Brüche vereinfachen müssen verstanden werden!
Auf einen Spickzettel gehören allgemeingültige Formeln, die man gerne vergißt oder durcheinanderwürfelt. Nichtsdestotrotz muss man in ihrer Anwendung sicher sein und die Grundlagen beherrschen - und da scheint’s bei dir zu fehlen, weshalb dir auch ein 100seitiger Spickzettel vermutlich wenig nützen würde.
Gruß,
Kannitverstan
der den Bruch auch vereinfacht nicht schön findet
Ne, du, das passt schon. In meinem Informatik-Studium durften wir zu bestimmten Klausuren auch so viele Bücher sogar mitnehmen, wie wir nur schleppen konnten, jeder von uns hatte einen ausreichend großen Tisch zur Verfügung ![]() , aber wie du geschrieben hast:
, aber wie du geschrieben hast:
Und genau das ist der Punkt: wenn man etwas nicht verstanden hat, nützen einem auch 'zig Bücher nichts. Auch keine hundertseitige Broschüre. ![]()
Mein letzter halbwegs vernünftig
Matheunterricht ist mehr als 6 Jahre her und die Themen, die in der Klausur vorkommen, hatte ich damals in dem Umfang nicht. Ich möchte mich gar nicht dafür rechtfertigen, aber es fällt mir halt schwer innerhalb von kurzer Zeit mir all das selbst anzueignen und wenns nur so Kleinigkeiten wie Brüche Auflösen sind.
Mein Dozent weiß halt, dass viele Probleme mit dem Fach haben, deshalb die Hilfsmittel, obwohl sie für die meisten vorne und hinten nicht ausreichen.
Die „9“ lässt sich herauskürzen, Zähler und Nenner lassen sich danach mit x^2 multiplizieren:
(1 - (100/x^2)) / ( x + 10 + 100/x^2)
(x^2 - 100) / (x^3 + 10x^2 +100)
Beim Zähler dann noch die binom. Formel anwenden: (x+10)(x-10) / (x+10)x^2 +100
Eine weitere Vereinfachung scheint danach nicht mehr möglich zu sein: Simplify[(9-900/x^2)/(9x+90+900/x^2)] - Wolfram|Alpha
mfg M.L.
Mein letzter Matheunterricht war 1990. Ok, im Grundstudium hatte ich auch noch ein paar Mathevorlesungen (die aber nichts mit Brüchen zu tun hatten), aber das ist auch schon über 20 Jahre her.
Das glaube ich dir, ABER:
Eben darum solltest du verstehen, was du machst, und nicht nur stumpf die Lösung abschreiben.
räusper Okayyy… Nur für mein Verständnis: Du studierst irgendwas, und das ist eine Übungsaufgabe für eine Mathe-Klausur im Studium? Oder reden wir von einer Ausbildung?
Und ja: „Brüche auflösen“ ist eigentlich Handwerkszeug, das ich einem Realschüler zumuten würde.Und zwar ohne Spickzettel. Das heisst, nein. Eigentlich würde ich Euch so viele handschiftliche Spickzettel schreiben lassen, wie Ihr nur wollt. Und dann würde ich einfach den Bruch im Nenner mit ner 20* vor dem x modifizieren und lustig gucken ![]()
Leuten wir Dir empfehle ich gerne die „Brücken zur Mathematik“ - die quälen die Leser nur minimal mit Herleitungen und Beweisen und haben unendlich viele Beispiele. Da das Werk recht bekannt ist, sollte das in Eurer Bibliothek vorhanden sein, und damit kann man eigene Lücken recht gut selbstständig stopfen.
*hoffentlich erinnere ich mich richtig und es passiert das, was ich erhoffe, hab’s jetzt nicht durchgerechnet.
Ich habe nicht kurz vor der Klausur angefangen mit dem lernen.
Und ich weiß wo mein Problem ist, ohne Rechenwege die ich nachvollziehen kann verstehe ich es einfach nicht, das war schon immer so. Aber mit einer vernünftigen Wegbeschreibug weiß ich, dass ich es kann und die Klausur sogar gut bestehen werde.
oder
(x-10) / (x2 + 100/(x+10))
Diese Kleinigkeiten muß man verstanden haben. Ein Spickzettel hilft da gar nicht. Bei meiner Vordiplomklausur in Statistik durfte man an Büchern, Skripten und Formelsammlungen mitschleppen, was man nur tragen konnte. Trotzdem (oder vielleicht auch gerade deshalb) lag die Durchfallquote bei gut 60%.
Sach’ ich doch!