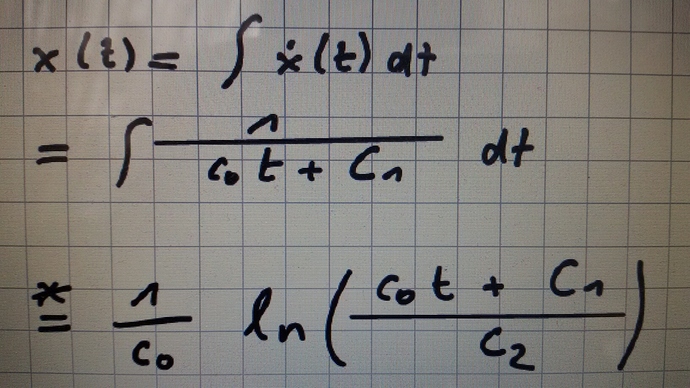Das ist nur ein Teil der Aufgabe und die Lösung, aber an dieser hänge ich gerade. Ich verstehe nicht wie man das integriert, ist das Partialbruchzerlegung? zu dem * Sternchen gibt es leider keinen Verweis.
Hallo!
Nein, das geht über Substitution. Das geht wie folgt:
Setze
u = (C_0 t + C_1)
Die Ableitung nach t ist:
du / dt = C_0 => dt = 1 / C_0 du
Das beides einsetzen:
Integral 1 / u * 1 / C_0 du = 1 / C_0 ln(u) +C
und zurück einsetzen:
1 / C_0 * ln(C_0 t + C_1) + C
Das C ist die Konstante, die beim Integrieren immer dazu kommt. Anscheinend wurde hier
C= - 1 / C_0 * ln(C_2)
gesetzt, so daß es zu deinem Ergebnis kommt. Das hängt von den Anfangsbedingungen ab, beispielsweise dem gewünschten Ort x(t) für t=0.
Hier nochmal, wie man auf die Substitution kommt:
Du kennst die Ableitungsregel „innere mal äußere“:
(f(g(x)))' = g'(x) * f'(g(x))
Integrieren ist die Umkehrung des Ableitens, daher:
f(g(x)) = Integral g'(x) * f'(g(x)) dx
Wenn du bei deinem Integral scharf hinschaust erkennst du, daß die Ableitung des Nenners - bis auf einen konstanten Faktor - dem Zähler entspricht. Demnach ist g(x) = C_0 * t + C_1 und f'(...) = 1/...
Und das legt die Substitution nahe.
(Das ist eine gewisse Übungs- und Erfahrungssache.)
danke für die antwort. ich verstehe es nur leider immer noch nicht.
ich habe die frage auch hier gestellt: http://www.mathelounge.de/326008/integrationsaufgabe-aufgabe-mechanik-beweung-massenpunktes
und da verstehe ich es auch nicht, aber ich finde es dort übersichtlicher dargestellt. Aber warum dt=dz/co? oder in deinem fall du/dt=co? das verstehe ich nicht.
Und ich versteh nicht warum integral 1/z dz = ln(z) ist. Und überhaupt wo kommt das 1/co her was dann auf einmal vor dem integral steht.

Also würde dir ein Buch empfehlen oder wenigstens auf YouTube nach Integrationstechniken suchen. Also bei deiner Aufgabe bietet es sich an zu substituieren. Das bedeutet ich ersetze etwas durch etwas anders. Meistens wird dafür der Buchstabe u gewählt. So also machen wir aus c0t+c1 einfach u. Jetzt würde ja da stehen: integral 1/u dt. So jetzt muss natürlich auch das dt substituiert werden. Und dabei gilt du/dt=u’. Das ausgerechnet gibt dt=1/c0 du. so das setzen wir dann wieder ein: integral 1/u1/c0du. Da 1/c0 einfach eine konstante ist kannst das einfach vor das integral packen. Jetzt muss man einfach auswendig wissen das 1/u die Ableitung vom Log ist. Somit ist der Log die Integration von 1/u. Damit haben wir 1/c0log(u)+c. Rücksubstituieren gibt 1/c0log(c0t+c1)+c. Zu deinem Ergebnis mit dem Stern also entweder wurde hier für die Konstante ein Wert angekommen oder es würde mit Grenzen integriert. Also das würde mir den Bruch erklären da ich ja die beiden Grenzen von einander abziehen muss. Naja hoffe konnte soweit helfen. Wie gesagt besorg dir ne Lektüre das ist auf der Hochschule/Uni überlebenswichtig. Lg