Hallo Wolke,
wo liegt den genau Dein Problem?
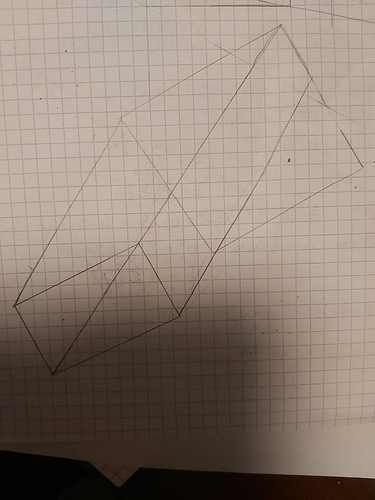
Also ich weiß nicht wie ich das zeichnen soll denn da kommt etwas komisches heraus.
Dann zeig doch mal, was rauskommt. Und nach Möglichkeit nicht gedreht wie die ersten Bilder, ich möchte mir nicht nochmal den Hals verrenken.
1 Like
Ehrlich gesagt, habe ich heute das erste Mal von zentrischer Streckung gelesen. Zumindest kann ich mich nicht daran erinnern.
Warum machst du dir das Leben unnötig schwer und zeichnest das Rechteck schräg? Habt ihr das im Unterricht so gemacht? Hier z. B. ist das Rechteck „gerade“:
https://sites.google.com/site/flonlines/howto/mathe-howtos/die-zentrische-streckung
Guck mal hier ab Minute 2:45 (aber ohne Ton, das verwirrt nur), da ist ungefähr das, was du brauchst, nur mit einem anderen Streckfaktor. Du musst ja die Länge verdoppeln und die Breite verdreifachen (wegen 2:3):
Versuch’s nochmal! Ich glaube, du hast einfach zu kompliziert gedacht!
1 Like
hi,
wäre es nicht sinniger, wenn sich das auf Original : Abbild bezieht?
Im Zusammenhang mit den anderen Fragen wäre es mir irgendwie logischer.
grüße
lipi
1 Like
Hallo,
können wir uns erstmal darauf einigen, dass es einfacher wäre, das Rechteck gerade und nicht schräg zu zeichnen? 
Meinst du, das Original wäre das Doppelte und das Abbild das Dreifache, also wäre der Streckfaktor 1,5? Möglich wäre das natürlich auch.
Ich kann mir vorstellen, dass @Metapher uns da „aufklären“ könnte. 
Mal gucken …
Gruß
Christa
1 Like
Nicht „auch“. Die Überschrift sagt „Ähnlichkeit“ - d.h. die Winkel sind gleich (alles rechte), Länge und Breite stehen im selben Verhältnis zueinander. Deine beiden Rechtecke wären nicht ähnlich. Aber Du hast recht, dass @anon83936923 da einfach zu kompliziert denkt. Quick&dirty - blaues Rechteck 5 cm * 3 cm, Streckungszentrum Ecke unten links, grünes Rechteck 5 * 3/2 cm * 3 * 3/2 cm. Streckfaktor ist also tatsächlich 5 * 3/2 cm / 5 cm = 3 * 3/2 cm / 3 cm = 1,5.
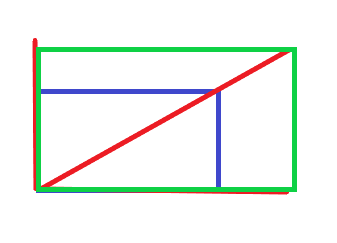
Freundliche Grüße,
Ralf
1 Like
Ich habe mich falsch ausgedrückt oder du hast mich missverstanden. 
Mit „auch“ meinte ich, es kann auch sein, dass lipi Recht hat (und ich implizit Unrecht).
Das stimmt. Trotzdem finde ich nicht gut, dass du die fertige Lösung, wenn auch
geliefert hast, denn @anon83936923 sollte das alleine (aber mit unserer Hilfe) hinbekommen.
Gruß
Christa
1 Like
Hallo,
„Vergrößern“/„Verkleinern“ eines Vielecks in Bezug auf einen vorgegebenen Punkt Z nennt man „zentrische Streckung“. Der Punkt Z ist dabei das „Streckungszentrum“.
Ganz allgemein zeichnet man dabei zunächst von Z aus zu jedem der Punkte A, B, C usw… des Vielecks je eine Gerade. Bei „Vergrößerung“ verlängert man diese Geraden über die Endpunkte hinaus. Auf diesen Geraden liegen nun die Strecken ZA, ZB, ZC usw. die nun jede für sich gestreckt wird. Das heißt: Jede Streckealt wird zu Streckeneu vergrößert. Und Streckeneu wird von Z aus abgetragen.
Die Streckung wird angegeben entweder
durch ein Streckungsverhältnis = Streckealt / Streckeneu
oder
durch einen Streckungsfaktor = Streckeneu / Streckealt
Der Streckungsfaktor ist also der Kehrwert des Streckungsverhältnisses.
In deinem Fall soll das Streckungszentrum Z auf einer der Ecken des Rechtecks A, B, C, D liegen. Sei also Z = A, dann führt das Rezept oben zu den Strecken ZB, ZC (= die Diagonale) und ZD. Weil Z = A ist das zunächst genau das vorhandene Recjteck selbst plus seine Diagonale.
Nun wird jede dieser drei Strecken vergrößert. Und zwar - jede nach Ausdrucksweise
im Verhältnis 2:3
bzw.
um den Faktor 3:2 = 1,5
Und die jeweilige Streckeneu wird, wie im allgemeinen Fall, von Z = A aus abgetragen. In deinem Fall, nämlich im Verhältnis 2:3, wird jede Strecke um die Hälfte verlängert:
Streckealt = 2 Teile
Streckeneu = 3 Teile
Wenn du die 3 neuen Endpunkte B’, C’, D’ verbindest, hast du das nun gestreckte Rechteck. @Tychiades hat oben schon gezeigt, wie das aussieht.
Gruß
Metapher
2 Like
Ich finde es „toll“, dass der Fragesteller seine „Antwort“, bei der nur das falsch erstellte Bild hochgeladen wurde, als „Lösung“ markiert hat, obwohl zwei richtige Lösungen in den Antworten zu finden sind. 
Oh tut mir leid ich wusste nich was das ist.
Jetzt weiß ich es und markiere gleich die Kommentare als Lösung.
Sorry
Hallo Christa,
Du hast natürlich recht und grundsätzlich finde ich das auch nicht gut. Hier war - wie die Zeichnung von @anon83936923 zeigt - das Problem ein falsches Verständnis der Aufgabe und vor allem des Prinzips ‚Ähnlichkeit‘. In dem Du ihn - entschuldige meine Offenheit - auch noch bestärkt hast, wobei das „auch“ nicht geholfen hat. Einfach um diese Verwirrung nicht noch zu vergrößern, schien mir das eindeutige Aufzeigen des richtigen Ansatzes sinnvoll.
Ich freue mich, dass @Metapher eine ausführliche Erklärung nachgeliefert hat und empfehle @anon83936923, diese zeichnerisch (mit Namen der Punkte und Strecken) nachzuvollziehen. Dann dürfte er das Prinzip (und nicht nur diese eine Aufgabe) verstanden haben.
Ansonsten - wenn jemand so höflich fragt und dann auch noch weiß. wie man ‚im Voraus‘ richtig schreibt … 
da konnte ich nicht widerstehen. Und - Deine Anmerkung wird künftig beachtet.
Gruß,
Ralf
Die berechtigte Kritik muss ich natürlich aiuch auf mich beziehen. Aber die @anon83936923 zeigte in. der eigenen Zeichnung ja, daß das ganze Verfahren noch nicht verstanden war. Sie hat die Diagonale verdreifacht, was bedeutet, daß sie (unter anderem!) noch nicht verstand, was mit der Anweisung „im Verhältnis 2:3 vergrößern“ gemeint ist (und außerdem natürlich, daß es sich auf jede Strecke separat bezieht). Also wollte ich das Verfahren erstmal überhaupt erklären.
Dann wurde aber klar: Mit so einer ausführlichen Erklärung löst man ja eh zugleich die spezielle Aufgabe. .Einer unmissverständlichje Erklärung war @anon83936923 aber offenbar weder durch eine Lehrperson, noch durch das Lehrbuch begegnet.
Zum Beweis, ob alles verstanden wurde, stehen der Wolke ja noch Aufgabe 1011 und 1012 zur Verfügung.
Gruß
Metapher
Ich muss zu meiner Schande gestehen, ich hatte die Überschrift „ausgeblendet“, als ich geantwortet habe. 
Ich mich auch, darauf hatte ich gehofft, deswegen hatte ich ihn auch gleich nach lipis Einwurf „vorbeizitiert“. 
ist aber nicht quasi die fertige Lösung, die du geliefert hast, aber du hast ja Besserung gelobt.
Wo du Recht hast …
Viele Grüße
Christa
Dieses Thema wurde automatisch 3 Tage nach der letzten Antwort geschlossen. Es sind keine neuen Nachrichten mehr erlaubt.