Der Mittelwert x ̅ =(x_1+x_2+x_n)/n
Warum minimiert der Mittelwert die Summe der Abstandsquadrate? 
was ist c?
Hoffentlich kann wer helfen 
Hast du doch geschrieben: c= x ̅ = (x_1+x_2+x_n)/n
Die Summe ist eine quadratische Folge in Abhängigkeit von c (die xi sind ja gegeben), die ihren Scheitelpunkt bei c= x ̅ hat.
Hallo,
die Gleichung ist ein Polynom in c (damit stetig differenzierbar). Extremwertprobleme erledigt man über die Ableitung (nach c):
(x_i - c)^2 = X^2 - 2cX + nc^2 (X = \sum x_i)
Ableitung Null setzen und umstellen:
2nc - 2X = 0 -> nc = X -> c = 1/n X
und 1/n X ist gerade der Mittelwert, wie oben definiert.
Das dies ein Minimum ist, ist klar, wenn man sich die Öffnung der Parabel anschaut, sie muß nach oben offen sein, da die Summe von Quadraten in R nicht negativ werden kann.
Hallo,
der Ausdruck ∑i (xi – c)2 wird hier als Funktion von c angesehen – man könnte sie „Summe-der-Abstandsquadrate-Funktion“ nennen. Die Variable c ist also das Argument der Funktion f© := ∑i (xi – c)2.
Wie man leicht einsehen kann, muss f nun für einen bestimmten Wert von c ein Minimum haben, und da fragt man sich natürlich, bei welchem Wert genau. Das kann man schnell ausrechnen (was Du am besten gleich selbst tust) und dabei kommt heraus, dass der gesuchte c-Wert gerade der arithmetische Mittelwert der xi-Kollektion ist, also c = 1/n ∑i xi.
Gruß
Martin
Danke einmal für alle Antworten!
Das hilft mir schon einmal weiter.
Was mir nicht klar war:
- Was ist ein Abstandsquadrat (einfach der Abstand zwischen den Ausprägrungen zum Quadrat)
- Was ist c (ist ein Argument von einer Funktion)
- Warum minimiert der Mittelwert die Summe der Abstandsquadrate (weil der Scheitelpunkt ist bei c=X ̅ und hier dieFunktion ihr Minimum hat
Also wenn das jetzt stimmt habe ich von allen Antworten was mitgenommen 
Sag bei nochmaligen lesen ist mir aufgefallen das ich die Auflösung des Polynoms nicht verstehe :-/
(Xi-c)^2 = a^2 -2ab-b^2 also x^2-2cx-c^2 und warum ist es nc^2 wieso kommt hier das n hinzu?
Vielleicht kommt manchen die Frage dumm vor aber ich verstehs nicht 
Das sind Summen über i, ich kann das hier nicht eintippen, aber (\sum c^2) von 1 bis n ist gleich c^2 + c^2 + ... + c^2 = n c^2.
Entschuldigung für dieses Wirrwarr. Links steht eine Summe, und rechts im Prinzip auch, da hab ich sie allerdings mit X abgekürzt.
Ok
weil es gerade zu dem Thema past,
dann ist wie in dem Beispiel Bild
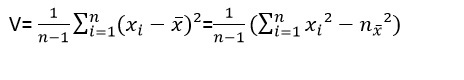
der Ausdruck in der letzten Klammer (Summe Nx^2 könnte ich auch Schreiben als "Summenzeichen"X^2
Sprich es sind 2 Schreibweisen möglich, so wie Xi und so wie Nx…
stimmt?
LG