Hallo Karl,
hab jetzt erst gesehen, daß dein Posting seit Wochen hier unbeantwortet vor sich hin dümpelte  Aber nun hast du ja schon eine erste Antwort bekommen …
Aber nun hast du ja schon eine erste Antwort bekommen …
Auch wenn Hans-Ulrich Keller Astronom ist und nicht theoretischer Physiker bzw. ART-Spezialist, müsste er wissen, daß die Aussage "
eine physikalisch unredliche und den Laien irreführende Aussage ist. Allerdings kommen so manche Spekulationen in den Medien über die „Geheimnisse“ der schwarzen Löcher auch daher, daß es sehr schwierig ist, die Ergebnisse der über ein Jahrhundert andauernden Arbeiten über die BH-Dynamik in anschaulicher Umgangssprache wiederzugeben.
Das Problem besteht/bestand darin, für die allgemeinrelativistischen Feldgleichungen
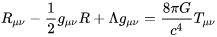
Lösungen zu finden. Ein erster Erfolg war die sog. Schwarzschild-Lösung, die unter extrem vereinfachten Randbedingungen den gravitativen materiefreien Umgebungsraum einer kugelsymmetrischen homogenen Masseverteilung (ungeladen, nicht rotierend). Zu dieser Lösung (Schwarzschild-Metrik) gehört der sog. Schwarzschild-Radius, der besagt, daß bei einer bestimmten Massendichte, nämlich wenn die Masseverteilung der Kugel einen bestimmten Radius erreicht, die Fluchtgeschwindigkeit = c wird. Die zugehörige Kugelsphäre ist in dieser Lösung eine mathematische Singularität (nicht die, um dies es in deiner Frage geht), d.h. darüberhinausgehende Aussagen (also zu kleineren Radien) war nicht möglich. Daher der Name „Ereignishorizont“. Weil aus dem Inneren dieses Horizontes auch Licht nicht entweichen könnte, also auch keine visuelle Information mehr nach außen dringen könnte, fand sich später die Bezeichnung „Black Hole“. Jede Spekulation, wie das Innere „aussieht“, ergibt sich von daher eh als abwegig. Auch für einen „inneren“ beobachter im gedankenexperiment ist es abwegig, da aus bestimmten Gründen auch innerhalb keine (Licht-)Information ausgetauscht werden kann (→ „asymptotic silence“)
Später wurde eine weitere Lösung der Gleichungen gefunden, die (ebenso ausschließlich) den Innenraum einer solchen Sphäre beschreibt, die ebenfalls an diesem Ereignishorizont eine Koordinaten-Singularität hat. D.h. es war noch nicht möglich, die Geodätische eines einfallenden Körpers über diese Grenze hinaus homogen zu berechnen. Erst durch eine andere Art von Koordinatensystem (→ Kruskal-Szekeres-Koordinaten) konnte eine allgemeine Form gefunden werden, in der diese Grenze keine mathematische Unstetigkeitsstelle mehr ist. Eine Unstetigkeitsstelle, eine Singularität, befindet sich jedenfalls im Zentrum dieses für einen Außenbeobachter sphärischen Raumgebietes. In dieser Singulariät ist die Raumkrümmung unendlich.
Nur: Jenseits dieser Grenze verkehren die Raum- und Zeit-Koordinaten ihre Bedeutung. Umgangssprachlich ausgedrückt: Zum Beispiel ein Raumpunkt wird zu einer Bewegungsgröße. Er ist keine „Stelle im Raum“, sondern eine Raumzeit-Kurve (das ist mit dem scherzhaften Ausdruck „Spaghettisierung“ gemeint). Und: Alle Geodätischen innerhalb dieser Sphäre enden notwendig in einem einzigen Punkt. Und an diesem Punkt ist die Raumkrümmung unendlich. Es gibt auch keine „stabilen“ Teilhorizonte innerhalb. Alle Horizonte kollabieren ihrerseits zu einem Punkt. Der „Raum“ ist also ein dynamisches Gebilde mit der Tendenz, sich selbst in einem (mathematischen!) Punkt zu „vernichten“. In den von Hawking und Penrose in den 1960ern entwickelten „Singularitäten-Theoremen“ wird interpretiert, daß alle Geodätischen sich zu einem einzigen Punkt entwickeln, an dem sie „nicht mehr fortsetzbar“ sind. D.h. sie enden in einem Punkt, und dieser Punkt befindet sich nicht mehr im Raum. Manche argumentieren, daß deshalb die ART keine „vollständige“ Theorie sei, weil eine „vollständige“ Theorie keine Lösung enthalten darf, an der sie nicht mehr gültig ist.
Später wurden auch andere Lösungen gefunden: Für rotierende schwarze Löcher, für geladene schwarze Löcher und für geladene und rotierende schwarze Löcher. Bei den rotierenden ist die zentrale Singulariät kein Punkt, sondern ein Ring von null Dicke.
Bis hierher nur zur Andeutung, daß es bei diesen Bemühungen weniger um
sich widersprechende Theorien
geht, als vielmehr um nach und nach gefundene Lösungen der Gravitationsgleichungen und en detail erweitere Möglichkeiten, diese physikalisch zu Interpretieren. Bis in die 1950er waren BHs nichts anderes als theoretische Lösungen der Gleichungen. Erst als man mehr über Sternentwicklungen wußte, wurden diese Konstrukte auch physikalisch brisant: Sterne kollabieren am Ende ihrer Entwicklung bis zu einem Zustand, in dem allein noch das → Paulische Ausschließungsprinzip fermionische Materieteilchen auseinander halten kann (Weiße Zwerge, Neutronensterne). Und Sterne über einer bestimmten Anfangsmasse durchschlagen bei ihrem Kollaps sogar diese Grenze der Materieverdichtung. Damit hatte man Kandidaten, die für eine Überschreitung ihres jeweiligen Ereignishorizontes in Frage kamen. Und in Konsequenz dann erst die Frage, was passiert mit den Materieteilchen jenseits des Ereignishorizontes?
Klar war, und ist nach wie vor, daß die Teilchen alle ihre Eigenschaften verlieren bis auf Masse, Drehimpuls und die elektrische Ladung. Und kaum strittig ist, daß - wie oben erwähnt - alle ihre Geodätischen den Singularitäten-Theoremen gehorchen müssen. Sie befinden sich nicht mehr zu einem „Zeitpunkt“ an einem „Ort“ bzw bewegen sich eine „Richtung“, sondern sie enden mitsamt der kollabierenden Raumzeit alle in einem Punkt der unendlich gekrümmten Raumzeit. Ist auch die Singularität mathematisch kein Problem, so ist sie einerseits ein Problem der Vollständigkeitfrage der Theorie. Aber sie ist jedenfalls ein Problem der Beschreibung der Materiezustände. D.h. die Frage, ob es vielleicht doch eine weitere physikalische Eigenschaft der Teilchen gibt, die, ganz anders als das Pauli-Prinzip, eine null-werdende Annäherung verhindert.
Und da gibt es noch viele weitere ungelöste Fragen. Z.B. die Einmischung quantenphysikalsicher Gesetze in dieses Szenarium: Z.B. Wieweit ist die Unbestimmtheitsrelation unter der Bedingung unendlicher Raumkrümmung noch relevant (unter anderem, weil der Begriff „Ort“ hier keinen Sinn mehr macht)? Ist die Unterscheidung zwischen Bosonen (die sich an ein und demselben Ort befinden können) und Fermionen (die das nicht können - Pauli-Prinzip) noch relevant? Da in der quantenfeldtheoretischen Behandlung der Elementarteilchen diese eh punktförmig sind („Volumen“, bzw. eine dementsprechende räumliche Größe, kommt ihnen erst durch ihre Wechselwirkungen zu): Was wird aus ihrer Wechselwirkung untereinander? Denn die wird durch Bosonen vermittelt (Gluonen usw.). Und überhaupt: Verliert der Wechselwirkungsbegriff selbst schon seine physikalische Relevanz, da er Bewegungsmöglichkeit vorraussetzt? … Nur halt ein paar Beispiele.
Aber: Das sind - vorerst - ungelöste Fragen. Und eine ungelöste Frage ist in den Naturwissenschaften etwas vollkommen anderes als „Fiktion“ und
kommt in der Natur nicht vor
Gruß
Metapher

 Aber nun hast du ja schon eine erste Antwort bekommen …
Aber nun hast du ja schon eine erste Antwort bekommen …