Spezielle Pyramidenform mit Regelmäßigem 3- & 5-Eck

[FelixFeuerdorn]

Hallo,

ich habe ein Problem ein 3D Objekt zu zeichnen. Und zwar soll es eines Art Kristall, wie man das auch von den „Sims“ kennt. Der Unterschied liegt darin das ich ein Regelmäßiges 5-Eck in der Mitte haben möchte, und jeweils ein Regelmäßiges 3-Eck, für die Obere und Untere Mitte, und natürlich ein Zentraler Punkt oben und unten.

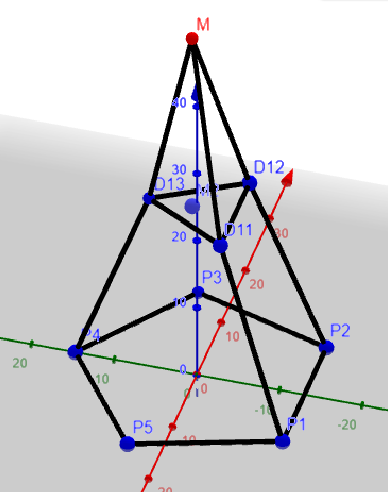
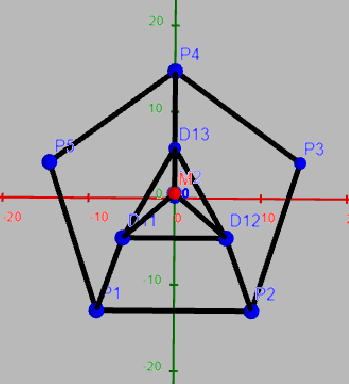
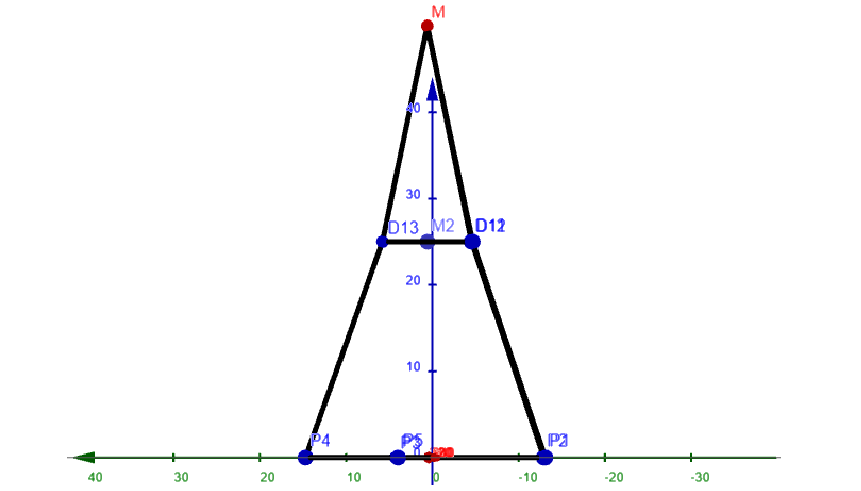
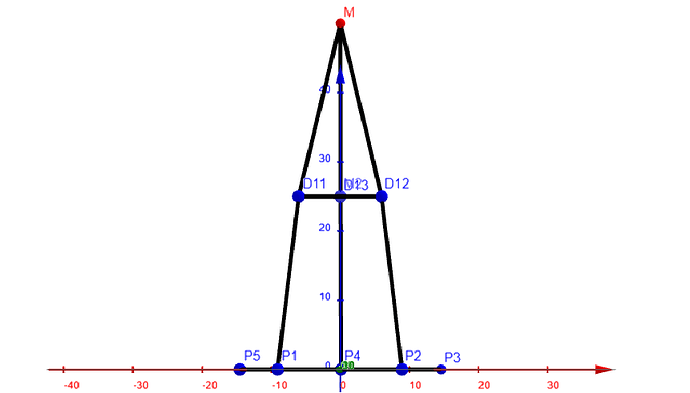
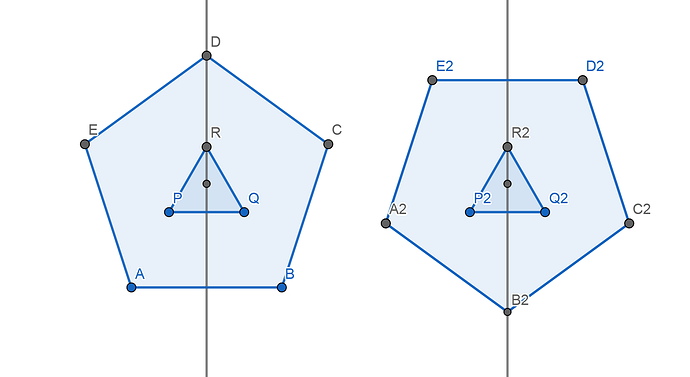
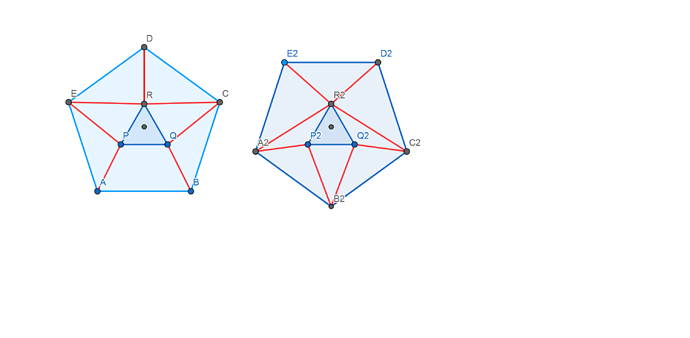
Ich habe damit auch schon mal angefangen, aber irgendwie ist das nicht das Ergebnis was ich haben will. Und fange meist immer wieder von vorne an. So wie jetzt, was bedeutet das ich nur die Bilder und keine genaueren Daten habe oder Live dabei sitze. Ich wollte diesmal einfach vorher einmal Fragen, ob jemand eine Idee hat wie man das richtig macht, sodass es auch schön aussieht.

Also nochmal zur genaueren Erklärung:
Ich möchte eine Pyramide erstellen, die im Z-Punkt gespiegelt ist. Dass soll dann halt wie ein „Kristall“ aussehen. Die Seite des 5-Ecks beträgt 20, die Seite des 3-Ecks beträgt 15, die gesamte Höhe beträgt 100, also 50 für eine Hälfte. Das 3-Eck befindet sich in der Mitte des 5-Ecks, auf genau in der mittleren Höhe also 25/75 (oder halt mit 25/-25 je nachdem wie man rechnet.). Als letztes sollen dann Ecken des 5-Ecks mit dem des 3-Ecks verbunden werden und die des 3-Ecks mit der Spitze. Nur stoße ich da auf Schwierigkeiten beim Aussehen. Die letzten beiden Punkte des 5-Ecks lassen sich nicht ordentlich verbinden, das sieht so nicht aus.

Hat einer vielleicht eine Lösung für mein Problem, muss auch nicht unbedingt mit GeoGebra gemacht sein, das sollim Endeffekt nur eine Skizze sein. Ich will das später als Symbol benutzen wir meinen Kram.

Es wäre echt gut wenn mir jemand einen Tipp geben könnte wie das zu schaffen ist.

Gruß Felix

[sweber]

Hi!

Du willst einen schönen, symmetrischen Kristall haben. Aber mit dem Dreieck und dem Fünfeck funktioniert das nicht, weil die sich nicht so schön symmetrisch zueinander legen lassen. Wäre es ein Sechseck, ginge es.

Denkbar ist schon, dass du alle Flächen als Dreiecke gestaltest, also noch die Graden P5-D11, P5-D13, P1-D12, P3-D12 und P3-D13 einzeichnest. Dann hättest du zumindest einen Körper mit Ebenen als Auzenflächen, aber symmetrisch wäre das auch nicht.

[Aprilfisch]

Servus,

jetzt nicht aus der Sicht der Geometrie, sondern der der Grafik:

Wenn es ums Aussehen geht: Wenn Du fünf Punkte auf der unteren Ebene mit drei Punkten auf der mittleren verbinden willst, kommst Du nicht daran vorbei, dass an zwei Stellen zwei Punkte unten mit einem oben verbunden sind, d.h. die Flächen des „Kristalls“ teils Vierecke und teils Dreiecke sind.

Den ins Auge fallenden Unterschied zwischen den schlanker wirkenden Dreiecken und den flächiger wirkenden Vierecken kannst Du ein wenig ausgleichen, indem du auch die Vierecke ein wenig schlanker erscheinen lässt: Probier mal, wie das herauskommt, wenn Du P1 mit D12, P2 und P3 mit D 13, P4 und P5 mit D 11 verbindest. Das gibt dann natürlich keine regelmäßige „Kristall“-Form, aber etwas, was vielleicht etwas harmonischer ausschaut.

Schöne Grüße

MM

[FelixFeuerdorn]

Wenn es anders gehen würde mit 6-Eck etc. hätte ich das ja gesagt, nur leider ist das so von mir gewollt weil ich es mir bisher nicht anders vorstellen kann mit 3- & 5-Eck.
Also Symtetrisch im Sinne von Oben und Untern würde mir ja schon reichen, aber ob das dann so gut aussieht ist die Frage.

[FelixFeuerdorn]

Es muss ja nicht unbedingt von Punkt zu Punkt sein, anfangs dachte ich ich könnte das 3-Eck 180 Grad gewendet besser verwanden, oder jetzt P3 und P5 einfach Mittig in zwischen D11-D13, D12-D13 setzen, dass sieht aber alles nicht so gut aus…

Und ich hatte ja gesagt das ich momentan nur die Bilder habe, also kann ich da momentan auch nichts verbinden.

[KeinesHerrenKnecht]

Wenn du ein gleichseitiges Fünfeck und ein gleichseitiges Dreieck übereinandersetzt, kann bestenfalls nur je eine Kante beider in einer Ebene liegen. Alle anderen sind windschief zueinander.
Bei der Verbindung der Eckpunkte ergeben sich zwei Dreiecke und drei Vierecke.
Das heißt, dass mindestens zwei der Vierecke zwei windschiefe gegenüberliegende Seite haben und „verdreht“ sind, d.h. nicht flach auf dem Tisch liegen können.
Warum sollen es denn gerade ein Fünf- und ein Dreieck sein?

[Aprilfisch]

Ja, regelmäßig ist da nichts zu machen.

Aber mal andersrum: Wie wichtig ist es denn, dass das Fünfeck kein Sechseck sein sollte? mit 3/6 könnte man viel hübscher arbeiten, und das regelmäßige Sechseck ist ja schon auch was.

Schöne Grüße

MM

[FelixFeuerdorn]

Also ich habe mir zum Spaß ein Magie-System überlegt im Sinne von RPGs, Geschichten etc. erst war es nur das 5-Eck als Magischer Zirkel, aber mit der Zeit sind weitere dazu gekommen.
Das Fünfeck bildet die „Elemente“: Wind, Wasser, Erde, Feuer, Energie (Elektrizität).
Die anderen möchte ich jetzt nicht dazu sagen, aber die bilden die 3-Ecken und die Spitzen. und Bisher sind mir keine „Grundlegenden Elemente“ eingefallen, die ich abgesehen von den Magiearten der 3-Ecken und der Spitzen dort einfügen könnte, deshalb habe ich das Fünfeck gewählt…

[Hexerl]

dann nimm doch als 6. Element die Zeit dazu (die ist auch in der Magie nicht ganz unwichtig) und schwubbs hast du ein gefälliges 6-Eck

[Metapher]

Ich sehe mal davon ab, daß das Ganze eine Spielerei mit Hobby-„Magie“ werden soll und nehme es als ein mathematisches Problem ernst (genauer: als eines von Symmetrie-Operationen im 3-dim Raum)

@FelixFeuerdorn

Dass soll dann halt wie ein „Kristall“ aussehen.

Du meinst damiit vermutlich, daß die durch die Kanten (= jeweils die Verbindungen zweier Ecken) erzeugten Flächen „eben“ sind. Mit „eben“ ist gemeint: Die Ecken liegen alle in einundderselben Ebene.

Nun liegen im 3-dim Raum 3 Ecken grundsätzlich in einer Ebene, 4 Ecken dagegen im Allgemeinen nicht. Damit geht es darum, die Ecken so zu verbinden (bzw. die Kanten so zu legen), daß ausschließlich 3-eckige Flächen entstehen.

Vorausgesetzt soll sein:

1. 3-Eck und 5-Eck sind gleichseitig
2. 3-Eck und 5-Eck liegen in parallenen Ebenen
3. Die Mittelpunke von 3-Eck und 5-Eck liegen mit der Spitze auf einer zu den Ebenen orthogonalen Geraden

Daraus folgt: Das 3-Eck bildet mit der Spitze eine symmetrische Pyramide, die mit dem 5-eckigen Pyramidenstumpf eine gemeinsame Figur bildet. Die Frage ist: Wie können die Kanten zwischen dem 5-Pyramidenstumpf und der 3-Pyramide gelegt werden, so, daß nur 3-eckige (bzw. nur ebene) Flächen entstehen.

Nun gilt Folgendes: n-zählige und m-zählige (koinzidente) Symmetrieachsen können, wenn n und m teilerfremd sind, nur in zwei möglichen Lagen kombiniert werden, so daß sie überhaupt eine gemeinsame Symmetrie bilden. Das Bild zeigt die zwei Lagen für n=3 und m=5

Die einzige Symmetrie ist dann die Spiegelsymmetrie an der hier einzig möglichen Spiegelebene (in der 2-dim Graphik die eingezeichnete Mittelsenkrechte).

In der linken Figur sieht man leicht: APQB bilden ein ebenes Trapez. Denn PQ ist parallel zu AB. Daß sie nicht beide in der Ebene der Grundfläche liegen, ändert daran nichts. In der rechten Figur ist ein solches Trapez nicht vorhanden.

Alle anderen Kanten, wie z.B. PR und ED in der linken, P₂R₂ und A₂E₂ in der rechten Figur, liegen „windschief“ zueinander (Fachausdruck für „nicht parallel und nicht in derselben Ebene“. Das bedeutet: Sie bilden keine ebenen Flächen, sondern solche, die in sich verdreht sind. Und für Flächen, die durch 5 Punkte gebildet werden, gilt das erst recht, zum Beispiel AEDPR in der linken Figur, A₂B₂C₂P₂Q₂ in der rechten Figur.

Das bedeutet: Alle anderen Punkte müssen so durch Kanten verbunden werden, die zugleich Kanten von 3-Ecken sind. Und das ist jedenfalls möglich, womit deine Aufgabe gelöst ist: Du hast ausschließlich ebene Flächen. Die Figur ist „kristallartig“ (obwohl das im kristallographischen Sinne natürlich kein Kristall sein kann):

Du hast also zwei Möglichkeiten für deine „kristallartige“ Doppelpyramide. Eine mit 7 und eine mit 8 Flächen (natürlich plus die 3 Flächen der oberen Dreieckspyramide)

Gruß
Metapher

[FelixFeuerdorn]

Vielen Dank, solch einen Tipp habe ich gebraucht.

Ich schätze so kann ich das ganze wirklich hinbekommen.