Statistische Frage zu Unfallzahlen

Wissenschaft Mathematik
#1

Hallo,

ich arbeite in der Sicherheitsabteilung eines Chemieunternehmens. Ich habe eine statistische Fragestellung. Leider habe ich nicht viel Ahnung von Statistik. Das statistische Wissen dazu habe ich mir im Internet angelesen, also bitte nicht wundern, wenn da ein paar grobe Schnitzer drin sind.

Zur Fragestellung:

In der Chemieindustrie zählt Sicherheit sehr viel. Die wichtigste Kennzahl dazu ist die Unfallzahl. Eigentlich eher die Anzahl der Unfälle (eines bestimmten Schweregrads) pro Mitarbeiterstunden bezogen auf das Unternehmen oder einzelne Abteilungen und einen bestimmten Zeitraum davon und normiert auf 200.000h (Total Recordable Incident Rate = TRIR). Aber wenn diese Daten näherungsweise gleich bleiben, können wir der Einfachheit halber mal bei der Unfallzahl bleiben.

Die Zahl wird für das Gesamtunternehmen, aber auch für einzelne Abteilungen erhoben um diese untereinander zu vergleichen (und den Bonus der Mitarbeiter zu bestimmen). Die Unfallzahlen konnten in den letzten 20 Jahren allerdings soweit gesenkt werden, dass in einer Abteilung nur noch wenige Unfälle pro Jahr passieren. Meine These ist daher, dass Änderungen in dieser Zahl keine Aussage über die tatsächliche „Sicherheitsleistung“ der Abteilung sind, sondern normale statistische Schwankungen. Die Kennzahl mag für das gesamte Unternehmen Sinn machen, aber nicht, mehr wenn man das auf einzelne Abteilungen runterbricht. Wenn beispielsweise die Unfallzahl von 120 auf 100 im Gesamtunternehmen sinkt, ist es etwas anderes als in einer Abteilung von 12 auf 10 Unfälle.

Nehmen wir mal an, die Unfallzahlen für die letzten 11 Jahre sehen in einer Abteilung so aus:

2006: 12
2007: 7
2008: 14
2009: 8
2010: 12
2011: 17
2012: 11
2013: 4
2014: 10
2015: 7
2016: 9

Meine These ist also, dass dies einer zufälligen Verteilung folgt. Begründen würde ich das mit einem Chi-Quadrat-Test als Anpassungstest auf eine Poissonverteilung. Also:

Poissonverteilung: grafik

Die beobachtete Häufigkeit wird zunächst in einer Tabelle aufgelistet:
grafik

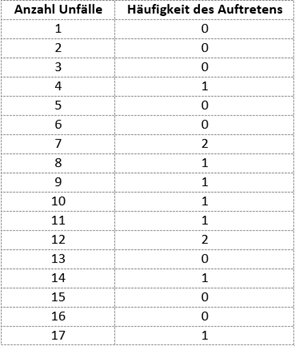
Anschließend werden die Werte in Klassen zusammengefasst und den erwarteten Werten nach einer Poissonverteilung gegenübergestellt:
grafik

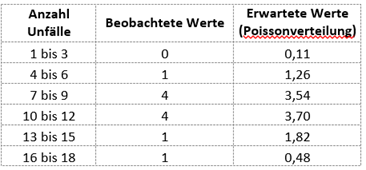
Mit einem Chi-Quadrat-Test als Anpassungstest

grafik

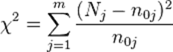
wird überprüft ob die beobachteten Werte einer poissonverteilt sind. Es ergibt sich eine Wahrscheinlichkeit von 95% dass dies der Fall ist.

Ist meine Schlussfolgerung richtig? Habe ich Fehler gemacht? Gibt es bessere Wege meine These zu überprüfen?

Vielen Dank im Voraus

#2

Hallo!

im Prinzip hast du das ganze richtig erfasst.

Die Sache mit dem X²-Test besagt jetzt aber nur, daß die Poisson-Funktion die Daten sehr gut beschreibt, aber nicht, daß die Daten tatsächlich poisson-verteilt sind.

Du hast da nur sehr wenige Daten in deiner letzten Tabelle. Die Anzahl der Zeilen mag für Poisson noch OK sein, die jeweilige Anzahl der beobachteten Werte ist sehr gering. Da könnte so auch ein Gauß gut rein passen: Die Daten sind nicht absolut,sondern Zufall. In der letzten Zeile könne genauso gut auch ne 0 stehen, und dann passt Gauß plötzlich besser als Poisson.

Ich würde daher nicht zu viel da rein interpretieren, auch wenn alles nach Poisson aussieht, und man daran eigentlich glauben möchte.

Hast du vielleicht Quartalszahlen? Damit bekämst du mehr Werte, und könntest etwas sicherer sein, daß das tatsächlich Poisson ist.

#3

Vielen Dank für die Antwort.
Ich habe noch eine andere Idee/Frage:

Gibt es vielleicht jenseits der Herangehensweise über die Poissonverteilung einen anderen Ansatz. Gibt es vieleicht so eine Art „Gesetz der kleinen Zahlen“ , das z.B. besagt: Bei seltenen Ereignissen sind auch größere Streuungen um den Mittelwert noch kein HInweis für einen Trend?

Vielen Dank