Statistischer Vergleich zweier Regressionsgeraden

Wissenschaft Mathematik
#1

Hallo zusammen :),

ich bin in einem anderen Thread schon mal auf eine ähnliche Problematik gestoßen, bin mir aber nicht sicher, ob die Problematik dort genau meine Situation darstellt.

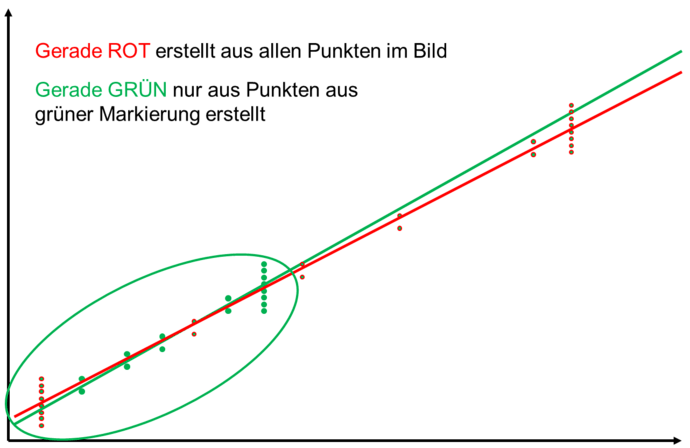
Mein Problem besteht darin, dass ich zwei Geraden (rot und grün) habe, die teilweise aus gleichen Werten erstellt wurden. Ich würde sie gerne daraufhin untersuchen, wie groß der Fehler ist, der gemacht wir, wenn die Gerade nur aus den Werten im grünen Bereich erstellt wird. Also wie groß der Untesrchied beider Geraden ist.

Geradenvergleich
Geradenvergleich1282×834 54.1 KB

Ich hoffe, ich hab mein Problem ausführlich genug geschildert.

Vielen Dank schon mal für die Hilfe!

Gruß
Jakob

1 Like
#2

Hast Du leider nicht. Ich sehe 2 Serien (rot und grün) von Werten, die gleiche x Werte haben. Das sieht aus wie Wiederholungsmessungen. Man sollte aber in Korrelationsmessungen einheitliche Messwertserien verwenden, also nicht Einzelmessungen mit Wiederholungsmessungen mischen. Dazu kommt, dass Du Messwerte diskriminieren willst. Also einmal alle Werte die in die Korrelation eingehen und in der zweiten Korrelation Messwerte aus unbekannten Gründen ausgeschlossen werden. Das ist sehr erklärungsbedürftig.
Der rechnerische Unterschied in den Geraden ergibt sich im unterschiedlichen Korrelationskoeffizienten sowie den unterschiedlichen Achsenabschnitten, die durch die Geradengleichungen ausgedrückt werden.
Udo Becker

#3

Hallo Udo,
Danke für die schnelle Antwort.
Vllt. hab ich mein Problem zu abstrakt dargestellt. Folgendes ist meine Sachlage:
Ich habe Messungen von niedrigen Lasten bis hin zu hohen Lasten. Durch alle Messpunkte lege ich eine Regressionsgerade (rote Gerade durch alle Messpunte). Was mich jetzt interessiert ist, wie groß ist der Fehler den ich mache, wenn ich zur Erstellung der Gerade nur die Punkte im grünen Bereich verwende und dann, hin zu hohen Lasten extrapoliere (grüne Gerade).
Es geht mir lediglich darum, wie ich am besten darstelle wie groß mein Fehler bei der Extrapolation ist.

Grüße Jakob

#4

Den Extrapolationsfehler kannst Du doch direkt ablesen: Die rote Gerade ist die „richtige“, die grüne die Extrapolierte. Also kannst Du auf der y Achse für jeden x Wert den absoluten Fehler (grün minus rot) ablesen und ihn in Prozent zum X Wert ausdrücken. Bei linearer Regression ist der Fehler in Prozent dann konstant und unabhängig vom X Wert (Last ?), wenn beide Geraden durch den Nullpunkt gehen. Im vorliegenden Fall schneiden sich die Geraden, meine Vermutung ist, dass es an der Messgenauigkeit liegt.
Im vorliegenden Fall wäre eine nichtlineare Regression wahrscheinlich besser. Die beiden Kurven wären vermutlich wesentlich besser übereinstimmend.
Udo Becker