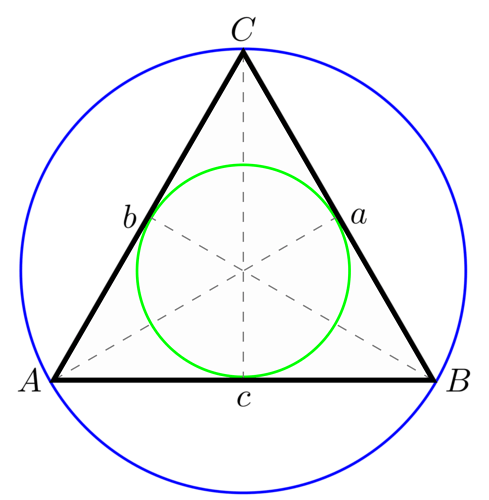
Ich weiß wie groß der Durchmesser des Kreises ist, auf dem Bild der grüne Kreis, und die Winkel des Dreiecks sind gleich. Mich interessieren die Länge der drei Seiten des Dreiecks.
Glaubst Du mir, daß die Strecke A-a genau r+R lang ist (r ist der Radius des Inkreises, R der des Umkreises)?
Wenn ja, dann schau Dir mal scharf das Dreieck A-C-c an, man kann hier mittels Pythagoras die Seite b in Form von (r+R) darstellen.
Fehlt noch R, richtig? Dazu schaut man sich das Dreieck A-M-c an (M ist der Mittelpunkt des In- und Umkreises).
Alles klar?
Das heißt bei einem Durchmesser von 120 wäre c-C 180 lang? Wenn ja, dann habe ich es fast ![]()
Jap, klingt gut. R zu r wie 2 zu 1, also R = 2r.
Zum Vorschlag von @hroptatyr zwei Alternativen:
Sei M = MittelpunktInkreis = SchnittpunktWinkelhalbierende
r = RadiusInkreis
R = [AM]
Mc = Mittelpunkt der Seite c, also [AMc] = c/2
Ferner:
Aus α = β = γ
⇒ a = b = c = gleichseitiges Dreieck
⇒(1) α = 60° und ⇒ ∠ MAMc = α/2= 30°
⇒(2) Winkelhalbierende = Seitenhalbierende ⇒ M = SchnittpunktSeitenhalbierende
Damit
Weg 1:
in ▵ AMMc : tan(α/2) = (d/2)/(c/2) = d/c
⇒ c = d/tan(30°) = d cot(30°) = d√3
Weg 2:
M = SchnittpunktSeitenhalbierende teilt die Seitenhalbierende im Verhältnis 2/1
⇒ [AM] = 2r = R
⇒ in ▵ AMMc : R² - r² = (2r)² - r² = (c/2)² ⇒ c = 2r√3
Gruß
Metapher