Wie hoch ist die Wahrscheinlichkeit

Wissenschaft Mathematik
#1

Hallo,

ich benötige Hilfe zu einer eher simplen Wahrscheinlichkeitsermittlung und bin dankbar, für den Lösungsweg. Hier die Aufgaben:

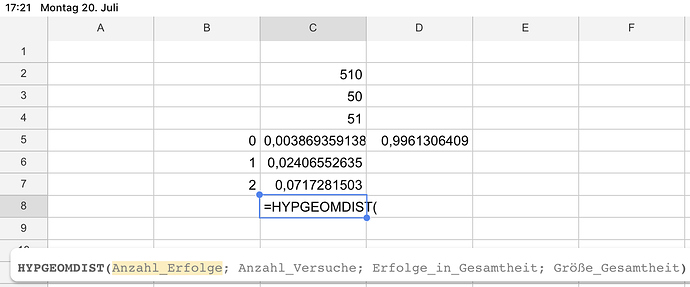
Bei einer Produktion von 510 Schrauben sind 50 Schrauben schlecht.
Die Endkontrolle prüft zufällig 10% (51) der Menge auf das Merkmal. Die schlechten Schrauben sind derweil unter den guten vermischt. Es wird also eine Menge von 51 entnommen (ohne zurück legen)

Wie hoch ist die Wahrscheinlichkeit, dass die Endkontrolle zumindest EINE schlechte Schraube findet?

Vielen Dank für den Lösungsweg.

#2

DAs ist vergleichweise einfach:

Die Wahrscheinlichkeit keine schlechte Schraube zu finden ist 460/510 (ca. 90,19%). Wenn man das Experiment 51 mal wiederholt und dabei nicht zurücklegt ist das also

460/510 * 459/509 * 458/508 * […] * 409/459

Die Wahrscheinlichkeit, keine schlechte Schraube zu finden liegt also bei 0,387% - die Wahrscheinlichkeit mindestens eine schlechte Schraube zu finden im Umkehrschluss also bei 99,613%.

1 Like
#3

Vielen Dank.
Ich habe das versucht mit der hypergeometrischen Dichteverteilung zu rechnen. Vielleicht war das etwas zu kompliziert angesetzt.

#4

Im Prinzip passt das schon

Bild
Bild1575×657 133 KB

1 Like
#5

Hallo,

eine HGV liegt hier vor und Du kannst es auch damit rechnen:

pHGV(k) = (M über k) · (N – M über n – k) / (N über n)

Mit „zumindest EINE schlechte Schraube“ ist in Deiner Aufgabe nach 1 – pHGV(0) gefragt für die Parameter N = 510, M = 50 und dem Stichprobenumfang n = 51.

Für k = 0 ist (M über k) = 1 und p(0) somit gleich

p(0) = (N – M über n) / (N über n)

Wenn Du nun die beiden BK jeweils nach Definition als Fakultätenbruch ausschreibst, wird sich ein n! wegkürzen und was dann noch da steht, kannst Du als 460!/409! dividiert durch 510!/459! darstellen. Wegen 460!/409! = 460 · 459 · 458 · … · 410 ist das identisch mit dem von Zerschmetterling angegebenen Produkt – wenn es korrekterweise bei 410/460 stoppen würde, statt bei 409/459.

Also: Alles easy… :wink:

Gruß
Martin

1 Like
#6

Hallo,

Dein Produkt hat einen Faktor zuviel – es muss schon bei 410/460 stoppen.

8! / 5! = 1·2·3·4·5·6·7·8 / (1·2·3·4·5) = 6·7·8

Gruß
Martin

1 Like