Wie kann ich ein diese Vektorfunktion bilden?

Wissenschaft Mathematik
#1

Guten Tag liebe Mitmenschen.
Ich würde nun gerne folgende Frage stellen:
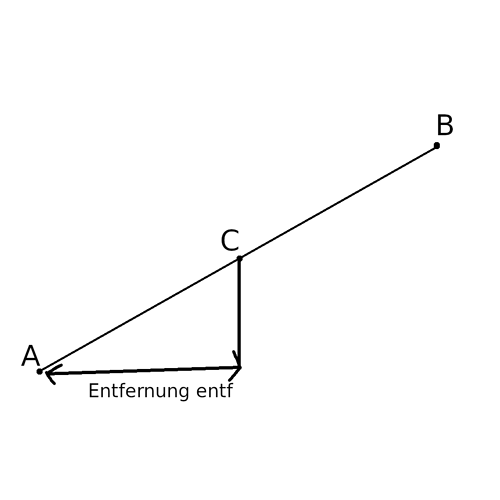
Wie kann ich mit 2 gegebenen Punkten A(x,y,z) und B(x,y,z) eine Funktion entwickeln, mit deren Hilfe ich einen Punkt (wir nennen ihn mal C(x,y,z)) auf einer Geraden oder einem Vektor zwischen A und B verschieben kann mittels einer Variable, in die ich eine Zahl einsetze, wie z.B.
100cm. Damit das nicht zu einfach ist ist bei der Verschiebung auch
noch zu beachten, dass die Z-Achse außer Acht zu lassen ist. Das heißt
die Punkte sollen die gewünschte Entfernung nur auf der X und Y Achse haben.

Der Input für die Formel wären also A(x,y,z),B(x,y,z) und entf(die gewünschte Entfernung vom Punkt A zu C nur unter der Berücksichtigung der X und Y Dimensionen).

Das Ergebnis der Formel sollen die Koordinaten des Punktes C(x,y,z) sein.

Ich bedanke mich natürlich schoneinmal im Vorraus für die Mühen und hoffe, dass es jemanden gibt der mir helfen kann.

Alle Grammatik und Rechtschreibungsfehler sind gewollt und dienen der allgemeinen Belustigung.

Unbenannt
Unbenannt1080×1080 16.7 KB

#2

Hallo,
ist das eine Hausaufgabe? Dann lege ich Dir die Punktrichtungsform ans Herz. Dein A ist Wikipedias p, Dein (B-A) ist Wikipedias u.

Für die Projektionen auf die X,Y-Ebene empfiehlt sich die Orthogonalprojektion, zumindest lese ich das so heraus.

#3

:weary: ?

#4

Edit:
Ah Entschuldigung, Du willst gar nicht C’ (Dein rechter Pfeil) ausrechnen, sondern B auf die XY-Ebene durch A projizieren (Orthogonalprojektion), es entsteht B’, dann entlang AB’ entf Schritte gehen, es entsteht C’. Dann C’ auf AB projizieren, so daß der Winkel AC’C ein rechter ist, richtig?

Also: Punktrichtungsform von AB’ ausrechnen, dann s (Wikipedia) auf entf/Norm(B-A) setzen. Das ist C’. Dann die Gerade g bilden, mit C’ als Stützvektor und u die Z-Achse (oder der Z-Einheitsvektor). Dann den Schnitt von g und AB ausrechnen (gleichsetzen).

1 Like
#5

Also mein Ziel ist es den Punkt C herauszufinden indem ich Punkt A und B zusammen mit einer gewünschten Entfernung in einer Funktion eintrage

#6

Gibt es Verständnisprobleme?

#7

Richtig, hab ich auch so verstanden. Ich sehe Du programmierst, also vielleicht doch keine Hausaufgabe. Also ich würde A zum Ursprung machen, dann ist (B-A) ohne die Z-Komponente Dein B’. entf/Norm(B’-A)*B’ der Punkt C’ (die Projektion auf die XY-Ebene), und dann kann man eigentlich mit der Definition des Cosinus die „Höhe“ CC’ ausrechnen, Winkel sind via Skalarprodukt definiert. Das ist die Z-Koordinate, die man noch in C’ einträgt, damit man C erhält.

Alles klar?

1 Like
#8

LösungZuVektorProblemPNG

Ich habe aus einem Matheforum diese Lösung bekommen und probiere sie gerade aus

#9

Ach übrigens, das mit dem programmieren war richtig. Ich werde mich jetzt daran machen es in C++ als Funktion zu schreiben.

#10

jo, sieht richtig aus. C++, weil es schnell gehen muß? Da gibt’s noch einige numerische Fallstricke, z.B. wenn Norm(B’ - A) sehr klein ist, weil B z.B. über/unter A hängt, also deren XY-Schatten fast der gleiche Punkt ist.

Z.B. A=(0,0,0), B=(1e-16, 1e-14, 1000)
In einem solchen Fall dreht man die XY-Ebene „geeignet“, aber wenn man das macht kann man auch gleich alles so drehen, daß AB in der Ebene liegt, dann ist Dein C’ auch Dein C.

Kostet natürlich Zeit. Also schnell und evtl. ungenau oder langsam und immer gleich korrekt.

1 Like
#11

Auf die Genauigkeit kommt es nicht so sehr an. Jedoch muss ich ehrlich zugeben, dass ich deinen Ausführungen zur Berechnung leider nicht folgen kann… Mir hat jemand in einem Mathe Forum die Formel gegeben die ich vermutlich mit dem was aus der Oberstufe hängen geblieben ist in C++ umsetzen könnte. Falls du viel Zeit hast dann würde ich mich freuen wenn du mir sowas wie einen Pseudocode schreibst der das verständlich macht.

#12

Die Fehler die Entstehen sollten beim Ergebnis(dem Punkt) hinter dem Komma passieren, dann ist alles in Ordnung