Hallo!
Ich habe mir das jetzt mal angeguckt, und schreib das nochmal zusammen.
Aufgabe
Es gibt korrespondierende 2D-Koordinaten von Punkten im Koordinatensystem eines Beamers (b )und einer Kinect (k).
Es soll eine Transformation gefunden werden, um die Koordinaten aus den Koordinatensystem Beamers in das der Kinect umzurechnen. Du hattest mir weitere Koordinaten per PN geschickt, daher gibts insgesamt diese Werte:
b_i=
[[36. 28.]
[46. 17.]
[50. 11.]
[46. 26.]
[35. 35.]
[34. 41.]
[31. 27.]
[34. 42.]
[51. 1.]
[54. 12.]]
k_i=
[[ 0.084 0.342]
[-0.71 0.34 ]
[-1.08 0.3 ]
[-0.577 0.13 ]
[ 0.36 0.267]
[ 0.59 0.11 ]
[ 0.67 0.83 ]
[ 0.74 0.14 ]
[-1.36 0.59 ]
[-1.4 0.17 ]]
Die Transformation soll mit der Methode der kleinsten Quadrate gefunden werden.
Grafisch
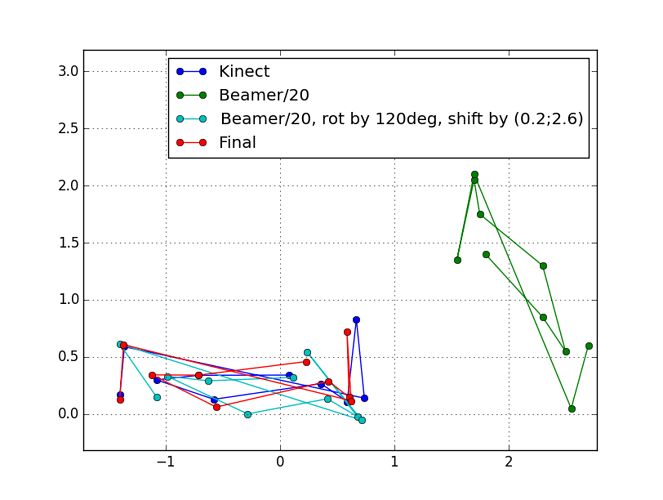
Hier sind die gegebenen Koordinaten mal grafisch aufgetragen. Die des Beamers wurden schonmal durch 20 dividiert, damit das vernünftig in ein Diagramm passt. Hier wird das Ergebnis schon etwas vorweg genommen:
Transformation
Eine Matrix M alleine ist nicht ausreichend, es bracht mindestens noch einen Verschiebungsvektor s, sofern der Ursprung beider Koordinatensysteme nicht gleich ist. Die Transformation sollte also so aussehen:
k=M*b+s
Startwerte
Es ist für einen Optimierungsalgorithmus immer gut, wenn man die zu optimierenden Werte schon halbwegs gut vorgibt, denn dann sind weniger Optimierungsschritte nötig. Sehr oft versagt so ein Algorithmus auch, wenn man keine passablen Startwerte angibt.
Schaut man sich die Daten Diagramm an und spielt ein wenig damit, passt zusätzlich zum Faktor 1/20 eine Drehung um 120° sowie eine Verschiebung um (0,2; 2,6) schon ganz gut (cyan). Eine Verzerrung hab ich nicht vorgegeben.
Das ist jetzt per Hand gemacht, kann man natürlich auch automatisieren. (Idee: Suche zwei Koordinaten, die möglichst weit voneinander entfernt sind, und berechne den Winkel dazwischen. Die Differenz der Winkel in beiden Koordinatensystemen ist dann die notwendige Drehung. Also die einen Koordinaten alle um den Winkel drehen. Danach Mittelpunkt aller Koordinaten bestimmen, die Differenz ist dann der Offsetvektor)
Optimierungsfunktion
Der Algorithmus versucht durch Variation der Parameter (Elemente der Matrix und des Offsetvektors), bestimmte Ergebniswerte zu minimieren. In dem Fall macht es Sinn, den Abstand zwischen Beamerkoordinaten nach der Transformation und Kinectkoordinaten zu minimieren. Im Idealfall ist der ja für alle Punkte 0. Deshalb habe ich eine Funktion geschrieben, die die Transformation durchführt, und dann eine Liste der Abstände zurück gibt.
Der Algorithmus gibt die Parameter vor, guckt sich die Ergebnisse an, dreht etwas an den Parametern, schaut wieder auf die Ergebnisse, …und so weiter, bis er meint, daß die Parameter gut sind.
Ergebnis
Folgendes kommt dann raus, wenn ich das Problem lösen lasse.
Die Punkte sind in rot in der Grafik oben, und man sieht, das das eigentlich ganz gut aussieht. Der erste Punkt liegt ziemlich daneben, genauso wie die beiden rechten. Man könnte bei den rechten fragen, warum die Daten nicht noch mehr in die Breite, nach links gezogen wurden. Aber dann würden die beiden Punkte bei x=0,5, die jetzt schon zu weit links sind, noch weiter nach links gezogen. Das passt also.
M= [-0.07513453 0.0174213 ]
[-0.04600035 -0.03105147]
s= [2.44682097]
[2.98529246]
Mal mit dem letzten Punkt ausprobiert, das ist der ganz links (unten):
[-0.07513453 0.0174213 ] * [54] + [2.44682097] = [-1.40140902]
[-0.04600035 -0.03105147] [12] [2.98529246] [ 0.12865592]
Das passt gut zur Koordinate [-1.4, 0.17] der Kinect, der y-Wert ist was klein, das sieht man auch in der Grafik.
Residuen
Residuen sind die Ergebniswerte der Optimierungsfunktion, sprich, in dem Fall die Abstände zwischen den transformierten Koordinaten des Beamers und denen der Kinect:
[0.18744622
0.00349813
0.05809584
0.07110722
0.07022332
0.04159181
0.1364712
0.11829252
0.01975152
0.04136749]
Auch hier zeigt sich wieder, daß der erste, der siebte und der achte Punkt einen deutlich größeren Abstand hat.
Nochmal zu den Daten:
Kinect und Beamer hängen mit etwas Abstand unter der Decke, wie ich deiner PN entnehme. Da deiner Koordinaten nur zweidimensional sind, führt das zu folgendem Problem: Der Beamer mag vielleicht senkrecht nach unten auf einen Stapel Käsescheiben leuchten. Dabei ist es egal, wie dick der Stapel ist.
Die Kinect schaut von der Seite auf das ganze, und da ändert sich die Koordinate der obersten Scheibe natürlich mit der Dicke des Stapels!
Das heißt, natürlich kann das auch theoretisch nie zu 100% passen!
Code
Ich hab das ganze in Python gerechnet. Das kann mit numpy ganz gut mit Matrizen etc. umgehen, sicher kann man sowas auch in C# realisieren. Die einzig wichtige Abhängigkeit ist ne Bibliothek mit dem least-squares solver.
Eins sehe ich grade: Ich habe in diesem Code um 130° gedreht, oben waren es nur 120°. Das führt zu minimal anderen Ergebnissen.
from math import *
import numpy as np
from scipy.optimize import leastsq
# data
kinect=np.array([[0.084, 0.342], [-0.71, 0.34], [-1.08, 0.3], [-0.577, 0.13], [0.36, 0.267], [0.59, 0.11] , \
[0.67, 0.83], [0.74, 0.14], [-1.36, 0.59], [-1.4, 0.17]], dtype=np.double).transpose()
beamer=np.array([[36, 28], [46, 17], [50, 11], [46, 26], [35, 35], [34, 41] , \
[31, 27], [34, 42], [51, 1], [54, 12]], dtype=np.double).transpose()
# functions
def transform(x):
'''Apply matrix and offset to all points from b and return result.
One can to the transformation for all points in b in one go!'''
mat=np.matrix([[x[0], x[1]],[x[2], x[3]]])
offset=[[x[4]], [x[5]]]
result= mat.dot(beamer).getA() + offset
return result
def residuum(x):
'''Calculates distance between transformed beamer and kinect coords
This function must have exactly one parameter, being a 1d array of values'''
diff= kinect - transform(x)
ret=[]
for i in diff.transpose():
ret.append(sqrt(i[0]**2 + i[1]**2))
return ret
print("b=")
print(beamer.transpose())
print("-"*20)
print("k=")
print(kinect.transpose())
print("-"*20)
########################
# guess: Rotate by 130, divide by 20, and shift a little
a=130.0
rotation= np.matrix([[cos(radians(a)), sin(radians(a))], [-sin(radians(a)), cos(radians(a))]]) / 20
shift=np.array([[0.2],[2.6]])
guess= rotation.dot(beamer).getA() + shift
#########################
# Initial parameter values - 1d array of parameters
x=np.concatenate((rotation.getA(), shift), axis=None)
print("Start values:")
print(x)
print("-"*20)
# Here, run the solver:
result=leastsq(residuum, x)
print("Final values:")
print(result[0])
print("M=")
print(result[0][:4].reshape(2,2))
print("s=")
print(result[0][4:].reshape(2,1))
print("-"*20)
print("Residuum:")
print(residuum(result[0]))
#########################
# This is just for drawing:
import matplotlib
matplotlib.use('TkAgg')
import matplotlib.pyplot as plt
plt.grid(True)
plt.axes().set_aspect('equal', 'datalim')
plt.plot(kinect[0], kinect[1], 'bo-', label='Kinect')
plt.plot(beamer[0] / 20, beamer[1] / 20, 'go-', label='Beamer/20')
plt.plot(guess[0], guess[1], 'co-', label='Beamer/20, rot by 130deg, shift by (0.2;2.6)')
final=transform(result[0])
plt.plot(final[0], final[1], 'ro-', label='Final')
plt.legend()
plt.show()
![]()
![]()