Winkel einer Welle in einer Nabe mit Spielpassung

[H3R0]

Hallo zusammen,

ich habe folgendes Problem:
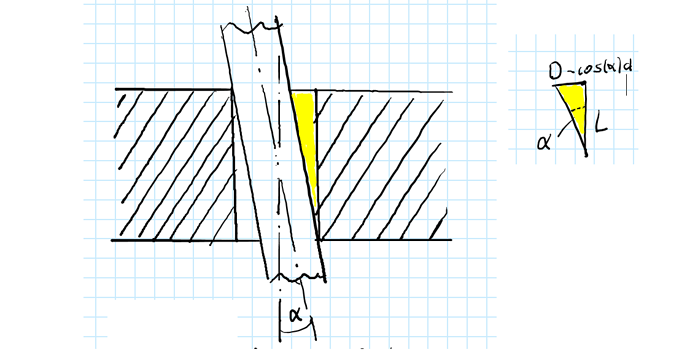
Eine Welle mit Durchmesser d ist in einer Nabe mit Durchmesser D gelagert, die Nabe hat eine Länge L.
Ich benötige den Winkel alpha, wie in der Skizze eingezeichnet.
Auf Grund des Winkels ist der Durchmesser d auf die Ebene des Durchmesser D projiziert gleich d’ = d * cos(alpha).
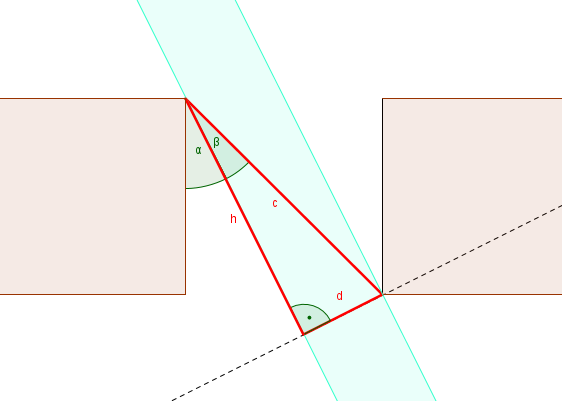
Leider ist für das markierte Dreieck mit der Gegenkathete gleich D - d’ der Winkel alpha abhängig von alpha.
Stimmt das soweit?
Wie kann ich den Winkel Alpha berechnen? (Keine Angst vor Differenzialgleichungen etc. ^^)

[sweber]

Hallo!

Erst einmal:

D-d*cos(a) für die obere Kathete ist nicht korrekt. Denn: Die vertikale Projektion des Durchmessers auf eine waagerechte Ebene ist kleiner als der Duchmesser!

Zeichne durch den oberen, linken Berührpunkt von Lager und Welle eine waagerechte Linie, sowie eine senkrecht zur Wellenachse. Die bilden zusammen mit der Welle ein rechtwinkliges Dreieck, dessen oberer Winkel der rechte ist, das waagerechte ist die Hypothenuse h , und genau die ist ja gesucht. Es gilt dann:

d/h = cos(alpha)

oder

h=d/cos(alpha)

Die obere Seite des gelben Dreiecks ist daher

D-h=D-d/cos(alpha)

---

Ich habe aber einen anderen Vorschlag:

d ist bekannt.
c=sqrt(L² + D²)
beta=arcsin(d / c)= arcsin(d / sqrt(L²+D²))

alpha+beta=arctan( D / L)

alpha = arctan( D / L) - beta = arctan( D / L) - arcsin(d / sqrt(L²+D²))

[Anonym_b43a4cae6f13]

Hallo,

Differenzialgleichungen sind hier sicher keine nötig, nur das Lösen einer (wenn auch komplizierten) goniometrischen Gleichung.

Im gelben Dreieck ist ja tan alpha = (D - cos(alpha) d)/ L.

Das multiplizieren wir mit L cos alpha durch und erhalten:

L sin alpha = D cos alpha - d cos^2 alpha

Quadrieren:

L^2 sin^2 alpha = D^2 cos^2 alpha - 2 D d cos^3 alpha + d^2 cos^4 alpha

sin^2 alpha = 1 - cos^2 alpha benutzen und alles auf eine Seite bringen:

d^2 cos^4 alpha - 2 D d cos^3 alpha + (D^2 + L^2) cos^2 alpha - L^2 = 0

Nun x = cos alpha substituieren:

d^2 x^4 - 2 D d x^3 + (D^2 + L^2) x^2 - L^2 = 0

Für Gleichungen vierten Grades gibt es Standard-Lösungsverfahren. Diese benutzen und am Schluss die Substitution rückgängig machen. Reichlich viel Aufwand, aber machbar. (Ich werde das Gefühl nicht los, dass es auch einfacher gehen müsste, komme aber leider im Moment nicht drauf. )

Gruß,
Björn

[falk_klemm]

Das dreieck zum Satz des Pythagoras ergänzen. Gegeben sind dann h und p. h=D-d und p=Stärke der Platte. Und dann übern Winkelsatz Alpha ausrechnen. Zur Veranschaulichung zwei Links. Im Grunde läßt sich das zusammen mit den Wikelgesetzen und Kreisberechnung auf fast alles in der einfachen Geometrie anwenden. Dreieck ist klar. Jedes Viereck läßt sich in Dreiecke aufteilen. Und im Kreis bis auf die Umfangberechnung besteht der Rest aus Drei- und Vier-ecken. Das gilt selbst für ein N-Eck. http://mathematikalpha.de/wp-content/uploads/2016/05/aufg053.pdf und https://de.serlo.org/mathe/terme-gleichungen/gleichungen/trigonometrische-gleichungen/sinus-kosinus-tangens?gclid=CKzi347Rmc0CFRKNGwod7JMNrw