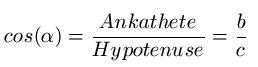Hallo, ich hätte eine Frage an euch Mathematiker,
wie ist die Formel wenn ich folgendes herausbekommen möchte:
Ein Konischer Zylinder hat an einer Stelle einen Durchmesser von 5 cm und der Konus einen Winkel von 3 Grad. Wie groß ist der Durchmesser wenn man 2 cm auf der Seitenfläche nach links geht (in die Richtung wo der Durchmesser kleiner wird). Ist das verständlich wie ich es meine?
Danke und Grüße
Hallo,
genügen dir diese Stichworte: Hypotenuse, Gegenkathete, Winkel?
Und ganz heiß: Cosinus
Vile Spaß beim lösen.
Hallo,
Sowas gibt es nicht. Ein Zylinder ist dadurch gekennzeichnet, dass Grundfläche und Deckfläche exakt gleich sind. Ein Ding mit kreisförmiger Grundfläche und geneigter Außenkante nennt man Kegel.
Die Kante der Außenfläche bildet mit der Grundfläche ein rechtwinkliges Dreieck (stell den Kegel auf die Grundfläche und betrachte ihn von der Seite!). Die Winkel des Dreiecks sind also 90°, 3° und 87°. Jetzt solltest Du die Länge der Seite ausrechnen können, die dem 3° Winkel gegenüberliegt. Um diesen Wert ist der Radius kleiner.
Grüße
Pierre
P.S.: Ich hoffe, mein Erklärungsmodell ist nich zu schwierig zu verstehen. Denn im Grunde ist es eine einfache Winkelberechnung.
Nein, leider nicht. Ich hoffte, es gäbe eine einfache Formel wo man jeweils die Werte einsetzen kann. Ich suche mal im Netz nach einem Onlinerechner. Danke trotzdem.
Ich habe was sinnvolles dazu gefunden, dass ich verwenden kann:
Danke an alle, Frage erledigt.
Na, da wäre ich ja mal gespannt, wie Du damit den Durchmesser der oberen Fläche ausrechnest…
Grüße
Das ist sicher eine der Abituraufgaben die neulich einen Protest ausgelöst hatten 
Möglicherweise. Und ohne Internetseite, wo man die Daten eingibt und ohne eigenes Nachdenken das Ergebnis ablesen kann ….
Ja, ich gebe zu, das ist ein zutiefst gehässiger Gedanke.
Grüße
Das war Quatsch, Sinus genügt, musste mein verschüttetes Wissen selbst erst auffrischen.
Da ich vermute dass es nicht um deine Hausaufgaben geht, dafür bist du schon zu lange angemeldet, hier das Ergebnis:
48,95328 mm, also 4,9cm.
Aber viel wichtiger ist der Rechenweg. Hast du es inzwischen?
Ganz einfach: Den Winkel weiß ich ja, also kann ich einfach solange den Durchmesser ändern bis der richtige Winkel rauskommt.
Na ja, solche Seiten sind wirklich praktisch. Mathe in der Schule ist bei mir über 30 Jahre her und für einen einzigen Anwendungsfall ist das schon gut.
Der Grund, warum ich so gehässig fragte (und dafür entschuldige ich mic): Bei der verlinkten Seite geht es nicht um die Berechnung der Eigenschaften von Kegelsegmenten. Hier geht es darum, einen Bastelbogen für ein Kegelsegment zu erstellen. Der Winkel, dem man sich nähern kann, ist nicht identisch mit Deinem Wunschwinkel.
So ergibt die Näherung, die Du vorhast, einen oberen Durchmesser von 49,67 für 3°.
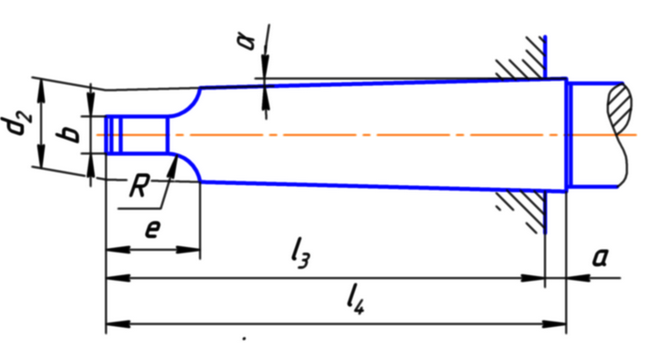
Wenn man das Kegelsegment von der Seite betrachtet, ist es eine Fläche (ein gleichschenkliges Trapez), was die Sache wesentlich einfacher macht. Wenn man die Grundfläche des Trapezes unten hat, könnte man links und rechts rechtwinklige Dreiecke einzeichnen. Von diesen Dreiecken kennen wir:
Hypothenuse (Seite gegenüber dem rechten Winkel): 20 mm
Beta (der Winkel gegenüber der Ankathete): 3°
errechnet wird Alpha (der Winkel gegenüber der Gegenkathete): 87°.
Wissen wollen wir den Wert der Ankathete.
Das ist die Formel zur Berechnung:
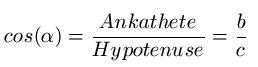
(Formel entnommen der Seite frutfrei-lernen)
Wenn man die Formel umstellt, erhält man
cos(𝜶)*c=b
also cos(87°)*20 mm=x mm
Die Grundfläche der kleinen Dreiecke beträgt also 1,047 mm. Diese muss man links und rechts von der großen Grundfläche abziehen. Dann ergibt sich, dass die obere Fläche unseres Kegelsegments einen Durchmesser von 47,906 mm besitzt.
Ich fürchte, dass @Bernd54 die Grundfläche des kleinen Dreiecks nur einmal abgezogen hat.
Bei mir ebenfalls. Das „Formelheft“ aus meiner Schulzeit liegt vergraben im Keller. Daher musste auch ich mir die Formeln aus dem Internet zusammen kramen (auch Begriffe wie Hypotenuse, Ankathete, gleichschenkliges Trapez …). Eistein wird der Satz zugeschrieben: Allgemeinbildung ist das, was übrig bleibt, wenn man die Details vergessen hat.
Nur leider nicht, wenn sie gar nicht nach der Lösung sucht, die Du brauchst.
Grüße
Pierre
Ich glaube, du machst einen Denkfehler.
Er will ja auf der Hypotenuse 2cm entlang gehen. Damit wird der Sinus zur Anwendung kommen.
Und ja, mit dem Winkel ist das etwas uneindeutig. Sind die 3° auf eine Seite bezogen oder auf die Kegelspitze? Ich bin von der Kegelspitze ausgegangen.
Also sin(3°) x 2cm oder sin(1,5°) x 2cm x 2.
Die Ergebnisse unterscheiden sich ab der 4. Kommastelle.
(hab mich in meinem ersten Ergebnis etwas verhauen, mal sehen, wer mich da korrigiert )
Edit: man sollte doch bis zum Ende lesen. Du hast ja 87° genommen, also doch Cosinus.
Ich verstehe nicht, worauf Du hinaus willst. Wenn der Kegel einen Winkel von 3° hat, dann hat er den ringsum. (Zumindest wenn man einen geraden Kegel annimmt.)
Grüße
Bei konischen Werkzeugaufnahmen (Morsekegel/Morsekonus) gibt man ja auch den Neigungswinkel an, das war mit halt geläufiger.
Aber selbst da geht doch der Neigungswinkel rund herum.
Guck dir mal links das mittlere Bild an, da ist der Winkel nur an einer Seite eingetragen.
Andernfalls müsste er an der hier nicht vorhandenen Spitze angetragen sein.
Ja, warum sollte in einer technischen Zeichnung eines Kegels der Winkel auch auf der zweiten Seite eingezeichnet sein. Per Definition hast Du am dreidimensionalen Objekt „gerader Kegel“ an allen Stellen der Außenfläche den gleichen Winkel.
Und wenn Du Dir die Zeichnung ansiehst, dann wirst Du sicher so wie ich erkennen, dass links wie recht eine Symmetrie vorliegt.
Ja, man könnte auf der Zeichnung oben und unten den Winkel eintragen. Niemand wird aber in einer technischen Zeichnung eines Hauses alle Meter eintragen, dass das Haus 14 m breit ist …
Grüße
Ok, danke nochmal an alle. Ich steig an dieser Stelle aus dem Thema aus😁
Eine Frage noch:
Bezog sich dein Beispiel zufällig auf einen Morsekegel?
Also auf eine Werkzeugaufnahme für rotierende Werkzeuge (Bohrer, Fräser etc.)