Hallo,
Vorsicht – langes Posting – Lesen auf eigene Gefahr! :–)
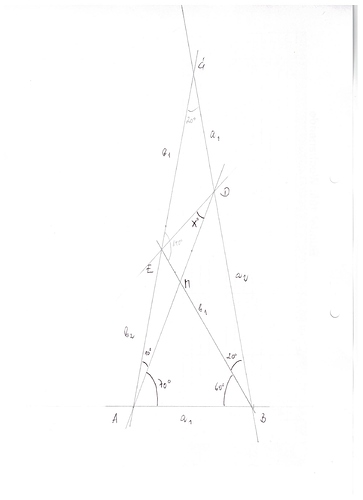
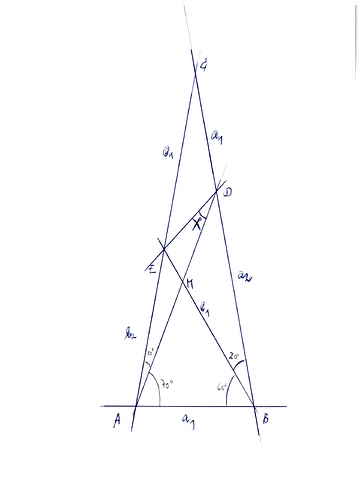
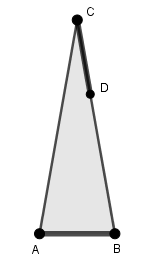
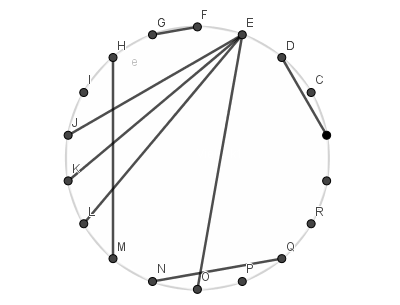
ich starte mit einem Bild des Konstrukts, in dem alles zunächst Überflüssige weggelassen ist (nämlich der Punkt E und die AD-Verbindungsstrecke):
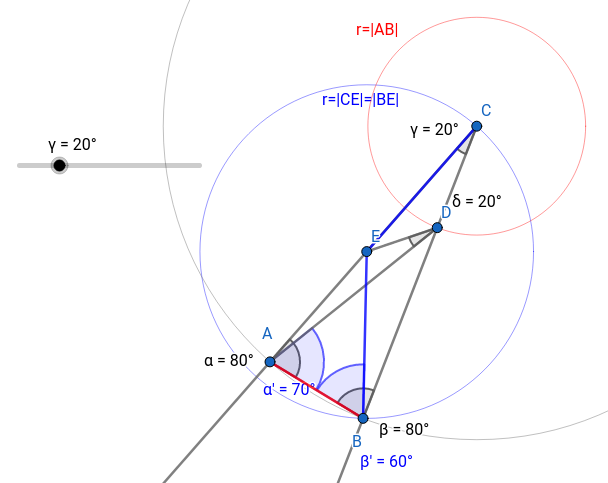
Vorgegeben ist: Das Dreieck ist gleichschenklig (C liegt auf der AB-Mittelsenkrechten), der Innenwinkel in C beträgt γ = 20° (woraus sofort die A- und B-Innenwinkel zu je 80° folgen)
und die Strecken AB und CD sind gleich lang.
Betrachte das Bild und frage Dich, was Du siehst. Du wirst mir zustimmen, dass zwei gleichlange dünne Strecken und zwei gleichlange dicke Strecken zu sehen sind. Wobei es einen Unterschied zwischen dem „Dünne-Strecken-Paar“ und dem „Dicke-Strecken-Paar“ gibt: Die dünnen Strecken teilen sich einen Punkt miteinander, aber die dicken tun das nicht.
Diese Tatsache hat nun eine ganz bestimmte Konsequenz: Wegen ihrer Längengleichheit („Kongruenz“) kann man sowohl die beiden dünnen Strecken als auch die beiden dicken aufeinander abbilden. Bei den dünnen Strecken geht das aber mit einer einzigen Klappspiegelung, wohingegen man bei den dicken Strecken zwei Spiegelungen benötigt.
Die Achse der „Dünnen-Strecken-Spiegelung“ ist klar, das ist die vertikale AB-Mittelsenkrechte des Dreiecks. Und die beiden Achsen der „Dicken-Strecken-Zweifach-Spiegelung?“ Wo die liegen ist vielleicht nicht ganz so offensichtlich, aber auch sie sind zu finden: Man muss einmal an der BC-Mittelsenkrechten spiegeln und dann nochmal an der Winkelhalbierenden der Strecken BA und BC.
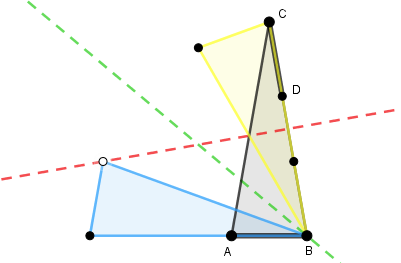
Jetzt wird es interessant: Was bekommt man denn, wenn man dabei die komplette Figur mitspiegelt? Die Antwort ist das blaue Dreieck in diesem Bild:
Das gelbe Dreieck (das nicht weiter interessant ist) ist das Ergebnis der ersten Klappspiegelung (Achse = die rotgestrichelte Linie), und das blaue Dreieck ist das Spiegelbild des gelben nach der zweiten Klappspiegelung (Achse = die grüngestrichelte Linie).
Wie Du siehst, liegt der Spiegel-Spiegelpunkt von A (weiß hervorgehoben) gerade auf der rotgestrichelten Linie. Zu diesem „merkwürdigen Zusammentreffen“ kommt es nur bei einem ganz bestimmten Dreieck-Öffnungswinkel γ, nämlich den 20°, die das Dreieck ΔABC tatsächlich (vom Erfinder des Rätsels aus diesem Grund absichtlich verpasst bekommen) hat. Diesen Gedanken kann man weiter verfolgen, aber ich möchte auf etwas anderes hinaus.
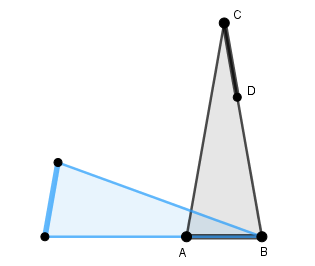
Wir haben durch unsere Spiegeloperation neue dünne und dicke Strecken erzeugt, und da wollten wir doch mal Inventur machen (nur graues und blaues Dreieck beachten): Haben wir jetzt drei dünne und zwei dicke Strecken? Nein, die „kurze“ Seite des blauen Dreiecks müssen wir natürlich noch dick machen:
Es sind also korrekt insgesamt vier dünne und drei dicke Strecken, von denen eine beiden Dreiecken gemeinsam „gehört“, nämlich die Strecke AB.
Einmal Spiegeln erzeugt also eine neue dicke Strecke. Würden wir die Spiegeloperation mit dem blauen Dreieck wiederholen, bekämen wir eine weitere dicke Strecke (und ein weiteres Dreieck, wenn wir es zeichnen). Dann das neue Dreieck wieder spiegeln und so fort und immer neue dicke Strecken kämen hinzu. Niemand verbietet uns, diese Spiegelungen zum Beispiel bis zur Nummer 509 fortzusetzen – und dann? Würden wir dann gut fünfhundert dicke Strecken auf dem Blatt Papier (oder dem Monitor) sehen? Die Antwort ist nein. Bei der siebzehnten Spiegelung passiert nämlich etwas wundersames: Die dadurch erzeugte dicke Strecke ist nicht mehr neu, sondern „alt“, denn sie fällt genau auf die Strecke CD!
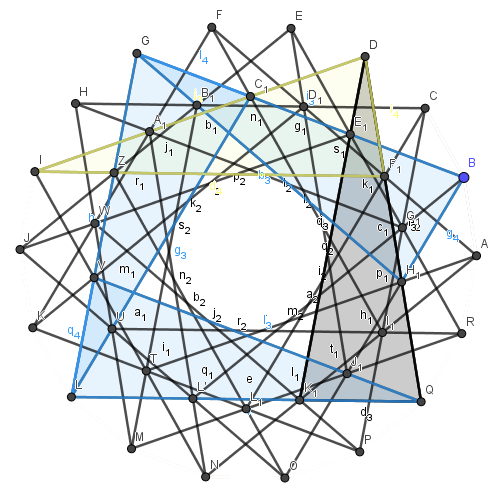
Das so erzeugte Gebilde sieht so aus:
Das graue Dreieck ist das Ausgangsdreieck, die blauen Dreiecke jene nach der ersten/zweiten/dritten Spiegelung und das gelbe Dreieck ist das letzte vor der Vollendung der Figur. Die Anzahl der Zacken dieses sonderbaren Sterns ist 18. Das hat natürlich seinen guten Grund: Das achtzehnfache des Dreieick-Innenwinkels 80° ist 1440° und das ist gerade das Vierfache des Vollwinkels 360°. Entsprechend macht man beim Spiegeln auch vier Umläufe, bis man den Stern vollendet hat.
Die Erkenntnis dieser ganzen Prozedur ist ziemlich verblüffend: Die Ausgangsfigur (das so harmlos aussehende allererste Bild) definiert ein regelmäßiges Achtzehneck!
Jetzt betrachte Dir die Linien genauer: Die Dreieckpunkte B und C fallen mit je einer Zacke des Sterns zusammen und dazwischen liegen genau vier Zacken. Die Dreieckseite AC kann man nach links unten etwas verlängern, dann trifft sie ebenfalls auf eine Zacke. Dazwischen liegen aber nicht vier, sondern „sechs“ Zacken.
Natürlich gibt es auch Verbindungslinien zwischen den Eckpunkten des Achtzehnecks, die zwei oder drei oder auch gar keine Zacken dazwischen haben. Zur Illustration sind in diesem Achtzehneck ein paar solcher Diagonalen eingezeichnet:
Was jetzt kommt, kannst Du Dir schon denken: Man zeichnet
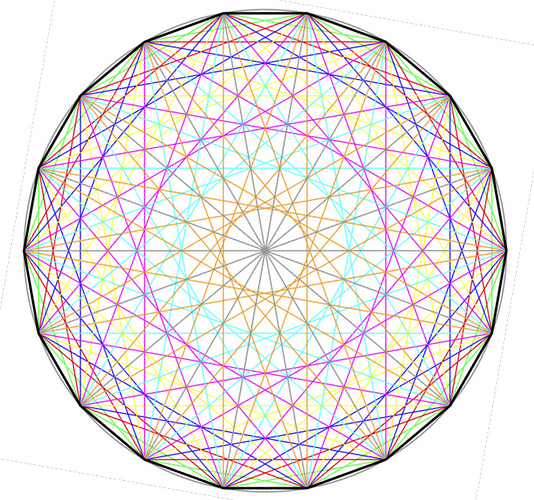
alle möglichen Diagonalen, die es überhaupt gibt. Dazu muss man jeden Eckpunkt mit jedem anderen miteinander verbinden. Dabei kommt ganz schön was zusammen, nämlich genau 135 Diagonalen (bei einem Achtzehneck) und hier siehst Du sie alle quietschbunt:
Selbstverständlich ist auch das Ausgangsdreieck noch vorhanden:
Nun ein ganz wichtiger Punkt: Die 135 Diagonalen schließen jetzt nicht etwa irgendwelche „krummen“ Winkel miteinander ein, sondern es treten nur 0, 10°, 20° usw., also
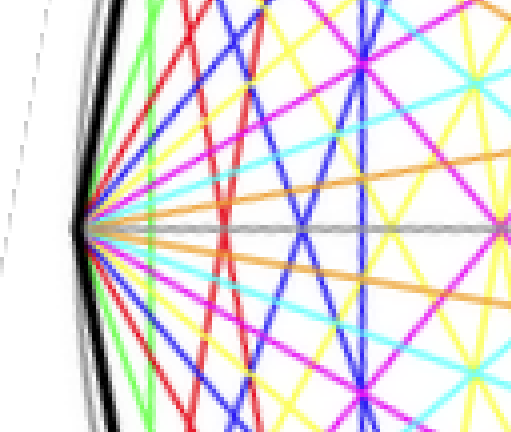
nur ganzahlige Vielfache von 10° auf. Man könnte sagen: Winkelmäßig herrscht in dem Kreis die allerbeste Ordnung, die man sich vorstellen kann (das ist nicht nur im Achtzehneck so, sondern in jedem regelmäßigen Vieleck). Hier ist die Umgebung einer Ecke vergrößert dargestellt:
Die von der Ecke nach rechts abgehenen 17 Diagonalen tun das unter den Winkeln –80° bis 80° in Zehnerschritten (gemessen gegen die Horizontale). Das gilt natürlich für
jede der achtzehn Ecken. Man spricht hier von sogenannten
Zentriwinkeln. Die haben noch eine Menge interessanter Eigenschaften mehr – Du kannst darüber ja in der Wikipedia nachlesen.
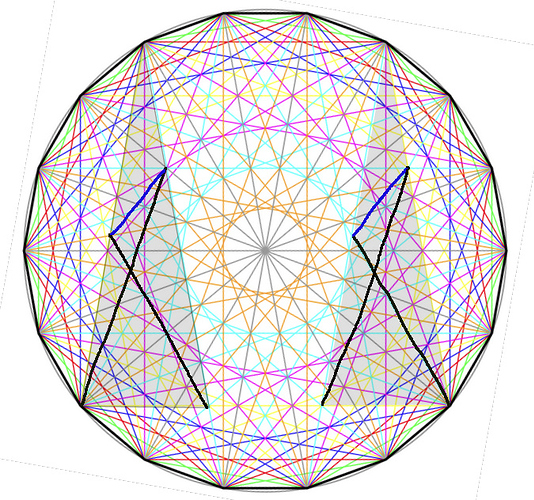
Nun können wir uns endlich um die Strecke AD kümmern. Wie wir wissen, schließt die (laut „Lösung“ des Rätsels) mit der Dreieckseite BC einen Winkel von 30° ein und die Dreieckseite ihrerseits gegen die Horizontale einen Winkel von 80°. Also hat die Strecke AD irgendeinen 10°-Vielfaches-Winkel und müsste somit doch auf einer der 135 Diagonalen in dem Stern liegen? Dies ist jedoch nicht der Fall. Der Grund dafür ist, dass der Punkt A, von dem die Strecke AD weggeht, kein Eckpunkt des Achtzehnecks ist. Aber wir können „woanders“ fündig werden. Das Dreieck kommt nämlich nicht nur rechts vor, sondern auch links noch einmal, und dann passt es:
Alle Punkte A, B, C, D, E fallen in beiden Dreiecken auf Diagonalenschnittpunkte. Die Strecke AD fällt im linken Dreieck auf eine magentafarbene Diagonale und die Strecke AE fällt im rechten Dreieck auf eine cyanfarbene Diagonale. Die Strecke DE dagegen fällt in keinem der Dreieck auf eine Diagonale.
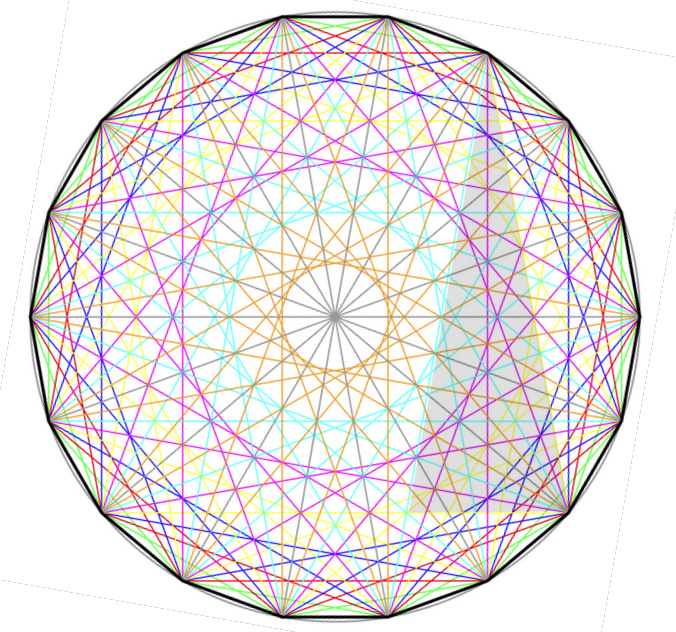
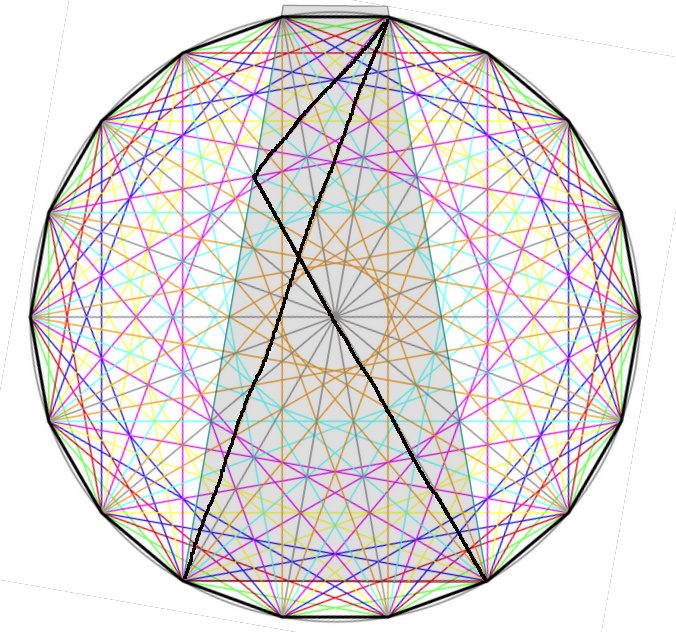
Als wenn das noch nicht genug wäre, hat das Achtzehneck noch eine Überraschung parat: Es enthält das Dreieck nämlich noch mehrfach an anderen Stellen in vergrößerter und verkleinerter Version (und damit meine ich nicht die je 18 gedrehten Varianten, sondern solche in derselben Ausrichtung!). Darunter befindet sich eines, das symmetrisch zur Vertikalen liegt:
In diesem „großen“ Dreieck liegen nun
alle Strecken (AB, BC, AC, BD, AE und sogar DE) auf einer der Diagonalen. Dadurch kannst Du jetzt tatsächlich alle Winkel einschließlich der im Rätsel gesuchten
direkt sehen, womit Deine Frage positiv beantwortet ist! Ein kleines Manko hat das große Dreieck allerdings: Es ragt oben über das Achtzehneck hinaus. Deshalb verbirgt es – im Gegensatz zu den beiden kleineren Dreiecken – die Längengleichheit der Strecken AB und CD. Irgendeinen Nachteil muss ja immer alles haben ;–)
Übrigens sind auch die Lösungs-Hilfskonstrukte, also z. B. das über die Strecke AB gebildete gleichseitige Dreieck im ersten Video, alle in den Diagonalen des Achtzehnecks versteckt. Wenn Du danach suchst, wirst Du sie selbst finden können.
Gruß
Martin