Dreieckskonstruktion

[ralf_g_nther]

Hallo zusammen. Bin da ein bisschen am Kloben bei folgender dreiecksaufgabe: b = 6 cm ,Winkel Beta = 40 Grad und der innenkreisdius beträgt 1,7 cm . . . .
Also: Winkel konstruieren mit 40 Grad mit 2 x Parallelen in den Innenseiten einzeichnen mit je 1,7 cm. Der Schnittpunkt der Parallelen ist der Mittelpunkt des Innenkrses.
Damit ist Winkel und innenkreisdius fertig.
Und dann kommt das hängen?
Satz des apollonius bringt nicht weiter.
Der Südpolsatz genausowenig. ( hier müsste er eigentlich " westpolsatz" heißen - kleiner Scherz)

Wie nun?
Wer kann helfen . .

LG Ralf

[Anonym_a5fb5cb73541]

Die Gegenseite liegt doch einfach am Inkreis an, oder möchtest Du es gern berechnen. Kunstruieren ist ja kein Problem.

[ralf_g_nther]

Danke für deine schnelle Antwort.
Klar, möchte ich die gegenseite b konstruieren. Geht über den thales satz. Aaaaaber: es sind b = 6 cm. . .

[Pontius]

Hallo,

1. Über b 110°-Fasskreisbogen (90°+ß/2) konstruieren.
2. Parallele zu b im Abstand 1,7cm (Innenkreisradius) ziehen —> Schnittpunkte M, M´(Mittelpunkte der Inkreise) mit dem Bogen.
3. Über b 40°- Fasskreisbogen konstruieren.
4. Gem. Südpolsatz schneiden sich die Winkelhalbierende von ß und die Mittelsenkrechte von b auf dem 40°-Bogen —> S (üdpol).
5. S über M bzw. M´hinaus bis zum jeweiligen Schnittpunkt mit dem 40°-Bogen verbinden —> B
6. A und C mit B verbinden —> gesuchtes Dreieck.

Gruß
Pontius

[ralf_g_nther]

Danke für deine Antwort. Werde mich gleich dran machen. Muss mich nur schlau mschen, was ein Fasskreisbogen ist. Wird aber schon werden. Trotzdem LG Ralf

[Martin]

Hallo Pontius,

yepp, this works. Man kann übrigens auch eine Lösung angeben, die ohne die Konstruktion der Fassbögen auskommt (aber dafür die des Inkreises beinhaltet). Das wäre meine Variante:

(1) Dreiecksseite b waagerecht^# zeichnen (Länge 6).
(2) „Obere“ b-Parallele im Abstand 1.7 konstruieren.
(3) Im „linken“ b-Endpunkt eine Gerade mit dem Winkel 90°–ß = 50° nach „oben“ konstruieren. Diese Gerade schneidet die in (2) konstruierte b-Parallele im Mittelpunkt M des Inkreises.
(4) Den Inkreis zeichnen (Mittelpunkt M, Radius 1.7).
(5) Von den beiden b-Endpunkten aus die Dreiecksseiten a und c als Tangenten an den Inkreis konstruieren.

^#Erklärung zu den Richtungsbegriffen: Weil die b-Dreiecksseite zwei Symmetrieachsen hat (nämlich sich selbst und ihre Mittelsenkrechte) gibt es vier spiegelbildlich zueinander liegende Dreiecke, die den Anforderungen genügen – ein „linkes oberes“, ein „rechtes oberes“, eine „linkes unteres“ und ein „rechtes unteres“. Meine Lösung beschreibt die Konstruktion des „linken oberen“ Dreiecks.

Gruß
Martin

[Pontius]

yepp, this works. Man kann übrigens auch eine Lösung angeben, die ohne die Konstruktion der Fassbögen auskommt (aber dafür die des Inkreises beinhaltet). Das wäre meine Variante:

Hallo Martin,

deine Lösung scheint mir, auch wenn bei meiner die Tangentenkonstruktionen entfallen, immer noch die ökonomischere zu sein.
Aber weil du für deine Tangentenkonstruktionen den Thaleshalbkreis brauchst, der ein Spezialfall des Fasskreisbogens ist, kommst auch du nicht ohne diesen aus.

Gruß
Pontius

[Martin]

Hallo Pontius,

OK dann schlage ich für die beiden Tangenten an den Inkreis folgende Konstruktion vor:

(5a) Zeichne um M einen Kreis mit dem Radius 3.4 = das Doppelte (!) des Inkreisradius 1.7.
(5b) Nimm von A aus die Strecke AM in den Zirkel und finde damit den Schnittpunkt X mit dem Doppelradiuskreis.
(5c) Zeichne die Gerade durch M und X. Sie schneidet den Inkreis im Tangentenberührpunkt für die Dreiecksseite c.
(5d) Wiederhole (5b) und (5c) entsprechend für den Punkt C.

Diese witzige (aber leider wenig bekannte) Doppelradiuskreis-Konstruktion für Tangenten an Kreise funktioniert tatsächlich. Ich schätze, Deine und meine Methode sind damit vom Aufwand her ungefähr gleichauf.

Gute Nacht (und Respekt für die Lösung dieser nicht ganz unanspruchsvollen Aufgabe)
Martin

[Martin]

Hallo Pontius und alle an diesem Thread Interessierten,

mir ist geboten, mich hier noch mal zu melden.

Als ich gerade etwas mit der Mathematiksoftware GeoGebra am Herumspielen war, habe ich mal versucht, meine Konstruktionsvariante damit umzusetzen. Statt eines Erfolgs bescherte mir das allerdings die Entdeckung eines Fehlers. Um es kurz zu machen: Deine Konstruktion ist korrekt, aber meine ist Schrott.

Der kritische Punkt ist meine Behauptung „Diese Gerade schneidet die in (2) konstruierte b-Parallele im Mittelpunkt M des Inkreises“. Das ist falsch, denn dieser Schnittpunkt fällt nicht mit dem Inkreismittelpunkt zusammen (und hat auch sonst keine Bedeutung). Beide Punkte liegen nur für die Parameter der Aufgabe (b = 6, ß = 40° und r_Inkreis = 1.7) zufällig sehr dicht beieinander. Davon hätte ich mich nicht in die Irre führen lassen dürfen – aber genau das ist passiert.

Wen die GeoGebra-Datei interessiert kann sie von mir per eMail bekommen. Die drei unabhängigen Punkte mit der Maus zu verschieben und zu beobachten, was sich in dem Konstrukt jeweils wie verschiebt, hat seinen Charme.

de.wikipedia.org/wiki/GeoGebra
www.geogebra.org

Gruß
Martin

[ralf_g_nther]

Hallo Martin,
auf diesem Punkt bin ich auch gestoßen. Denn die 50 grad Linie ist ja nicht die Winkelhalbierende vom Winkel cba. Das habe ich erkannt, nachdem ich den Radius vergrößert habe - und damit den Innenkreis.
Ich habe über das geometry pad einwenig herumgespielt und den Radius verändert. Dabei rutschte der Punkt c mit seinen 40 Grad Winkel auf dem großen Kreis herum.
Damit kann ja die 50 grad Linie nicht die Winkelhalbierende sein.
Aaaaaber: über den Südpolsatz erreichst du den Punkt c. ( also die Verbindung von 2 Punkten, nämlich den Schnittpunkt Umkreis und mittelsenkrechten mit dem Schnittpunkt 50 grad Linie mit der 1,7 cm Parallelen; beide Schnittpunkte verlängert ergibt den Punkt c auf dem Umkreis. )
Was ich nicht verstehe, ist folgendes: hast du den Punkt c, ist das Dreieck vollständig. Über die Winkelhalbierenden des Dreiecks bekommst du den Mittelpunkt des innenkreisdius des Dreiecks. Nur: dieser Mittelpunkt ist nicht der Schnittpunkt von 50 grad Linie mit der Parallelen von 1,7 cm.

Verstehst du, womit ich da ein Problem habe?

Teste doch mal einen Radius von 2 cm oder weniger an oder andersrum , verschiebe c auf dem aussenradius und passe den innenradius an. Du wirst dann sehen, wohin der Mittelpunkt des innenkreisdius wandert.

Antwort??

LG Ralf

[Martin]

Hallo Pontius,

Damit kann ja die 50 grad Linie nicht die Winkelhalbierende sein.

so ist es.

Aaaaaber: über den Südpolsatz erreichst du den Punkt c.

Ja. Wobei der gesuchte dritte Dreieckspunkt B ist, weil die b-Seitenlänge ja mit 6 gegeben ist.

also die Verbindung von 2 Punkten, nämlich den Schnittpunkt Umkreis und mittelsenkrechten mit dem Schnittpunkt 50 grad Linie mit der 1,7 cm Parallelen

Nein. Um den gesuchten dritten Dreieckpunkt B zu erreichen, musst Du eine Gerade durch den Südpol und den Schnittpunkt des 110°-Fasskreises mit der 1.7-Parallelen legen (das ist ja der Grund, warum man den 110°-Fasskreis überhaupt benötigt). Dieser Schnittpunkt ist der Inkreismittelpunkt und die Gerade durch ihn sowie den Südpol schneidet den Umkreis dann im Punkt B.

Die 1.7-Parallele wird natürlich auch von der 50°-Linie geschnitten, aber wie ich schon sagte: Dieser Schnittpunkt hat überhaupt keine Bedeutung. Ihn irrtümlich als Inkreismittelpunkt zu identifizieren war ja gerade mein Fehler.

Du wirst dann sehen, wohin der Mittelpunkt des innenkreisdius wandert.

Er wandert auf dem 110°-Fasskreis umher.

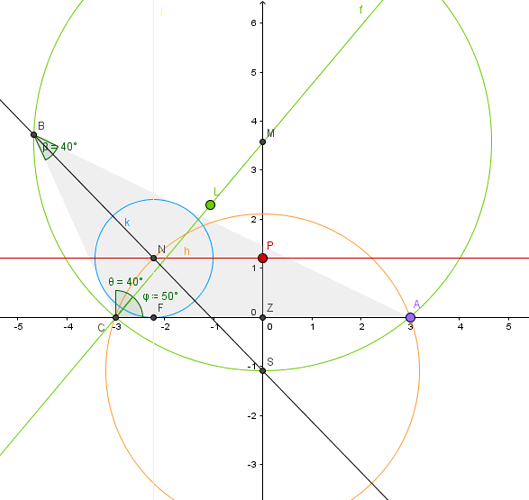
So sieht die Konstruktion für r_Inkreis = 1.2 statt 1.7 aus (bei 1.2 sieht man deutlich, dass die grüne 50°-Gerade am Inkreismittelpunkt vorbeiläuft):

Legende:
A legt b = |AC| auf 6 fest.
P legt |PZ| auf 1.2 (im Original: 1.7) fest.
L legt die 40° fest.

M = Umkreismittelpunkt
S = Südpol
N = Inkreismittelpunkt

Rote Gerade = die b-Parallele
Grüne Gerade = die 50°-Gerade
Grüner Kreis = der Umkreis (Mittelpunkt M, Radius |MA|)
Orangener Kreis = der 110°-Fasskreis (Mittelpunkt S, Radius |SA|)
Schwarze Gerade = die B-Winkelhalbierende
Gelbe Gerade = die b-Lotgerade durch N
Blauer Kreis = der Inkreis (Mittelpunkt N, Radius |NF|)

Gruß
Martin

[Pontius]

Hallo Martin,

vielen Dank für den Hinweis.
durch die zeichnerische Ungenauigkeit habe ich mich auch täuschen lassen.
Gem. Berechnung ist aber alpha/2 nicht 50°, sondern nur ca. 49, 506°.

Gruß
Pontius

[Pontius]

Deine Antwort sollte wohl an Ralf gerichtet sein.

[Martin]

Hallo,

Deine Antwort sollte wohl an Ralf gerichtet sein.

ja… Entschuldigung.

Gruß
Martin

[Martin]

(Diesmal richtig adressiert:) Hallo Pontius,

Gem. Berechnung ist aber alpha/2 nicht 50°, sondern nur ca. 49, 506°.

das würde ich gerne nachprüfen, kann aber alpha/2 gerade nicht zuordnen. Wo ist dieser Winkel, bitte?

Gruß
Martin

[ralf_g_nther]

Hallo Martin,
super Sache mit deinen Ausführungen.
Erscheint logisch und zielgerichtet .
Den fasskreisbogen und deinen orangenen Kreis werde ich mir nochmal zu Gemüte führen.
Vielen Dank für die Zeichnung.

LG
Ralf

Apropos Zeichnung.

Wie bekomme ich eine Geometry Pfad Zeichnung hier bei " wer weiß was " unter?
Und
Mein Problem ist die Tangentenbildung.
Wenn ich einen einheitskris habe mit M (0/0) und r= 1 und einen Punkt G bei (3/0) und möchte an diesen Kreis eine tangente legen, dann geht das ja über den thaleskreis. Sowie kein Problem. Nur jetzt technisch eine Linie von G auf den Schnittpunkt zu bekommen, das haut bei mir nicht hin. Das ist ein handwerkliches Problem, weil ich den Schnittpunkt nicht genau treffe.

Gibt es ein Hilfsmittel ???

[Pontius]

Was du natürlich nicht wissen konntest: Ich habe es bei meiner Zeichnung nicht so genau genommen, so dass A der linke und C der rechte Endpunkt der Strecke b ist.
Auf deine Grafik bezogen meine ich also den Winkel ACB/2 bzw. gamma/2.

[Martin]

Gem. Berechnung ist aber alpha/2 nicht 50°, sondern nur ca. 49, 506°.

Ach so, dort ist Dein alpha… ja, den Wert kann ich bestätigen. Auch ein halbes Winkelgrad Unterschied ist ein Unterschied.

Der Inkreisradius, bei dem der Inkreismittelpunkt tatsächlich auf die 50°-Gerade zu liegen kommt, lässt sich übrigens ganz leicht berechen; er beträgt r_Inkreis = 6/(cot(40°/2) + cot(50°/2)) ≈ 1.6729.

Schönes WE
Martin

[Martin]

Hallo Ralf,

Danke für Deine Wertschätzung :–)

Wie bekomme ich eine Geometry Pfad Zeichnung hier bei " wer weiß was " unter?

Ich fürchte, dafür bin ich der falsche Mann, weil ich von Smartphones und Tablets nur rudimentäre Ahnung habe. Auch die Software Geometry Pad kenne ich leider nicht. Auf meinem PC mach ich einfach – mit einem Utility namens Greenshot – einen Screenshot und füge die so erzeugte Grafikdatei in den Wer-Weiss-Was Editor ein.

Ich würde diese Frage einfach mal im Brett „iPad“ (Kategorie "Computer&Digital –> Mobile&Apps –> iPad) stellen. Wofür ist es denn sonst da? :–)

Das ist ein handwerkliches Problem, weil ich den Schnittpunkt nicht genau treffe.

Sorry, aber ich glaube, das nicht wirklich verstanden zu haben…

Schönes WE
Martin

[ralf_g_nther]

Hallo Martin,
Ich habe da noch verständnisprobleme mit deinem orangenen Kreis und den 110 Grad Winkel.
Den orangenen Kreis habe ich selber noch mal per Geometrie pad gezeichnet und das schein ja alles richtig zu laufen.
Um ein bisschen aufgeräumter zu sein, habe ich den 50 Grad Winkel auf deinem Punkt A gesetzt, dann hast du links mehr freies Feld.

Meine Datei suche ich anzuhängen in d Erwartung, dass das klappt.
Die Beschriftung stimmt nicht mit deiner überein, weil ich nicht wusste, wie man die Beschriftung ändert . . .

Gruß
Rlaf