Wie kann ich saisonale Schwankungen in Zeitreihen ermitteln und verifizieren?

Wissenschaft Mathematik
#1

Hallo Community,

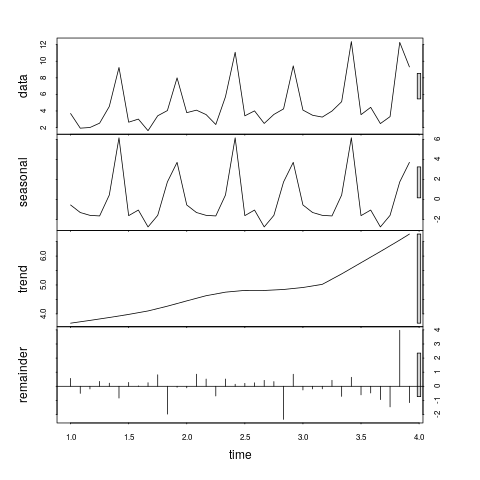
ich habe eine Reihe von Messwerten in zeitlicher Abfolge (lückenlos gemessen immer am Monatsersten). Zu diesen Messwerten habe ich ich die Regressionsgerade ermittelt und daraus resultierend die Abweichungen „Messwert vs (anhand Regressionsgerade) kalkulierter Wert“ ermittelt. So weit, so gut :smile:

Nun suche ich nach einem Weg, die Abweichungen zu analysieren, wobei mich folgendes interessiert:

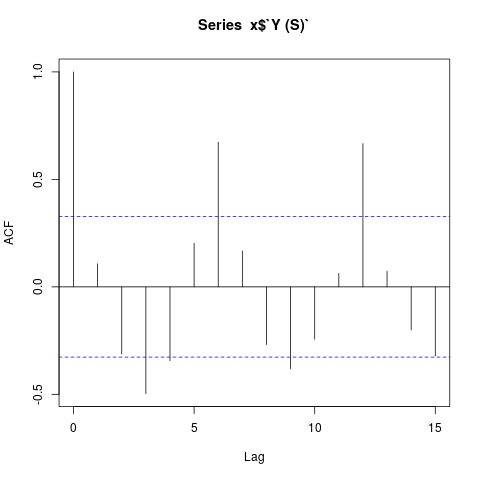
  1. Welche Monate fallen auf, weil sie regelmäßig „in die gleiche Richtung“ abweichen?
  2. Wie stark ist diese Abweichung?
  3. Sind diese Abweichungen signifikant oder möglicherweise zufällig?

Mein Ziel ist, nachher ein Modell (eine Formel, z.b. eine Modifzierte Regressionsgerade o.ä.) zu haben, welches auch die Schwankungen berücksichtigt, anhand dessen ich die Werte für die kommenden 12 Monate schätzen möchte. Ebenso möchte ich einen Wert haben, der mir sagt, wie genau dieses Modell auf die vorhandenen Messwerte zutrifft - was ich dann einfach als Indikator dafür hernehmen möchte, wie wahrscheinlich das auch als Prognose herhalten kann.

P.S. Ich hätte es gern möglichst einfach erklärt - ich bin zwar sehr interessiert an Mathematik, aber halt nur ein Laie :slight_smile:

Vielen Dank vorab!

#2

Hallo,
ganz allgemein geht das, indem man die Zeitreihe in z.B. 3 Komponenten zerlegt: Trend, Saison und Residual, das ist die Standardzerlegung des STL-Verfahrens.

Sagen wir Du hast eine additive Zerlegung X = T + S + I (falls multiplikativ, nimm Log). Dann kannst Du direkt in der S-Komponente (könnte man zu diesem Zwecke noch sortieren oder in in S_Jan, S_Feb, etc. aufteilen) Deine Fragen 1 und 2 beantworten. Die S-Komponente entlang der Zeit gemittelt (zusammen mit I) beantwortet dann auch Signifikanzfragen (Frage 3).

Die Implementationsdetails von STL (daneben gibt es auch unzählige andere Verfahren) sind vielleicht nicht so interessant, aber die Eckdaten:

  • Die Zeitreihe mit Lag k (laufendes k) wird mittels Loess-Fenster gesmootht (Du kennst k schon (12) und könntest hier z.B. einfach mitteln oder gleitend mitteln).
  • Wenn diese Saison-Zeitreihe feststeht, wird sie vom Original abgezogen und Period-on-Period gesmootht, z.B. mittels MA(1) oder EWMA. Das ergibt die Trendzeitreihe.
  • Die Summe aus Saison und Trend wird vom Original abgezogen und es verbleibt die Sporadische Zeitreihe (oder Residual- oder Fehlerzeitreihe).
#3

Vielen Dank für die Antwort … als Laie leider nicht unbedingt verständlich, aber ich konnte mir so einiges mit den von Dir genannten Stichworten zusammengooglen und mit viel Denkarbeit komme ich dann jetzt auf ein Ergebnis wie folgt:

  1. ich habe die Trendreihe ermittelt
  2. ich habe die Saisonschwankungen ermittelt
  3. ich habe die Restanteile ermittelt

Was ich allerdings an Deiner Antwort gar nicht verstehe, ist die Aussage „Die S-Komponente entlang der Zeit gemittelt (zusammen mit I) beantwortet dann auch Signifikanzfragen (Frage 3)“. Also ich verstehe weder, was „mit entlang der Zeit gemittelt“ bedeuten soll, noch erschließt sich mir der Sinn darin, einen (wie auch immer gebildeten) Mittelwert zu nutzen, um auf die Signifikanz zu schließen.

Kannst Du darauf noch näher eingehen?

#4

Was ich noch getan habe: ich habe das Bestimmtheitsmaß für den Trend ermittelt und auch für Trend+Saison. In der Regel ist das zweite Bestimmtheitsmaß größer als das erste - wenn auch meist nur minimal.

So weit, so gut :slight_smile:

Jetzt muss ich noch herausfinden, ob der Saison-Anteil signifikant ist (oder eben nicht). Zu dem Stichwort schlägt Google T-Test, F-Test und P-Test vor, allerdings ist mir nicht klar, welcher der richtige Test wäre und welche meiner ermittelten Werte ich da „einsetzen“ müsste, um herauszufinden, ob der Saison-Anteil signifikant (und somit unbedingt zu berücksichtigen) ist oder eben nicht (und somit der Trend ausreichend wäre).

#5

Also, erstmal Entschuldigung für die sehr dichte Darstellung, aber Du willst ja wahrscheinlich schnell ans Ziel und nicht erst Konzepte lernen. Auf der anderen Seite ist Desaisonalisieren natürlich ein Bereich, der ganze Bücher füllt und Arbeitsgruppen beschäftigt.

Also mit mitteln meine ich eigentlich ermitteln, sprich die Werte in S entlang der Zeit als stochaistischen Prozeß auffassen und dessen Parameter ermitteln. Im Gauß-Fall wären das Mittelwert und Varianz (wobei die S-Komponente ja per Konstruktion trendfrei sein soll, sprich der Mittelwert (der Differenzen) ist 0), die Fehlerkomponente (die Residuen) sollten ebenfalls keine Trendkomponente mehr enthalten, haben also auch Mittelwert 0. Bleibt sozusagen die Varianzen zu vergleichen.

Jetzt kenne ich naturlich Deine Daten nicht, Du mußt alles Gesagte auf Deinen Fall übersetzen. Mit dem ermittelten stochastischen Prozeß kannst Du nun Überlegungen zum Standardfehler (Sample-Varianz) anstellen, oder z.B. den Z-Test machen.

#6

Ah, Du bist schon weiter. Okay beim T-Test würde Deine Hypothese lauten: Wie dicht bin ich an den Residuen. Ein sogenannter paired sample t-test. Man kann aber auch herausfinden wollen, wie sehr unterscheidet sich meine Zeitreihe von einer nicht-saisonal beeinflußten Zeitreihe, sprich der Nullprozeß (mean 0, varianz 0), das macht man mit dem Einstichproben-t-test.

Man kann jetzt die gesamte Saisonkomponente untersuchen, das war was ich sagen wollte mit „entlang der Zeit“. Oder man kann auch die Signifikanz aller Januar-Saison-Werte, aller Februar-Saison-Werte usw. untersuchen, sprich 12 Signifikanztests machen.

Überhaupt ist das ganze Signifikanz-Thema nochmal eine Wissenschaft für sich. Hier gibt es kein Mach-erst-dies-dann-das. Nur als Ausblick verweise ich auf die Diskussion, daß P-Werte ohne Effektstärke bedeutungslos sind: https://en.wikipedia.org/wiki/Misunderstandings_of_p-values (englisch).

#7

Stimmt, dazu hätte ich ein paar Worte sagen sollen. Also: stelle Dir vor, Du liest jeden 1. eines Monats Deinen Stromzähler ab und notierst die Differenz zum Vormonat. So entstehen meine Messwerte.

Das bedeutet:

  1. die Messwerte sind ein zeitabhängig (je mehr Tage ein Monat hat, desto mehr Strom verbrauche ich bei gleicher täglicher Nutzung). Diese „Kalenderkomponente“ eliminiere ich, indem ich die Messwerte durch [Anzahl Tage des Messzeitraums] teile und mit 30 multipliziere.
  2. die Messungen können nur Werte >= 0 enthalten, da ein Stromzähler ja nicht rückwärts laufen kann

Das klingt nach dem, was ich anstrebe. Mein Ziel ist es, zwei „Formeln“ zu haben (einmal die Regressionsgerade T und einmal zusätzlich mit Saison-Additiv T+S). Mit dem Signifikanztest möchte ich herausfinden, ob S wirklich signifikant ist oder ob S auch mehr oder minder zufällig sind.

Oder anders ausgedrückt: wenn zum Beispiel S aussagt, daß Juni, Juli, August weniger Strom verbraucht wird und dafür November, Dezember und Januar mehr Strom verbraucht wird, dann will ich wissen, ob das " nur so aussieht" oder „wirklich so ist“ (=signifikant unterschiedlich von Zufall und signifikant unterschiedlich von nicht-saison-beeinflusster Zeitreihe).

Wie müsste ich den diesen Ein-Stichproben-t-Test aufsetzen? Der Link (und andere Google-Treffer) erklären das zwar - aber leider nicht auf einfache Weise (man muss schon echt viel Vor-Wissen aufweisen um das zu verstehen). Mir würde helfen, zu wissen: "nimm den Durchschnitt hiervon, teile es durch die Summe davon, bilde dann die Differenz zu irgendwas … ", dann krieg ich das sicher umgesetzt :smile:

Das wäre auch eine Möglichkeit. Wenn mindestens ein Monat der Saisonkomponenten als signifikant erkannt wird, dann wäre für mich auch die Gesamte S Reihe als signifikant zu betrachten und somit wäre die Frage beantwortet, ob ich S anwenden muss oder nicht (siehe Abschnitt 2).

P.S. Kann ich dir (per Mail o.ä.) eine Excel-Datei zukommen lassen, wo ich meine ganzen Berechnungen drin habe? Dann ist es vielleicht einfacher zu erklären, auf welche Spalten man Summen/Durchschnitte/etc legen und vergleichen muss …

#8

Erstmal ganz kurz:

Die Formel ist immer die gleiche, bei beliebiger Verteilung ändern sich lediglich Fehlerterme bzw. würde man verlangen, daß nach zentralem Grenzwertsatz eine hinreichend große Stichprobe vorliegt:

T = \sqrt{n} * (Xm - mu) / S

Mit Xm arithmetisches Mittel der Stichprobe, mu Erwartungswert der Grundgesamtheit, S empirische Standardabweichung.

Kannst mir die Daten gerne schicken, ich hab zwar kein Excel, aber das fummel ich mir schon hin. Email als PM.

Ohne die Daten gesehen zu haben, schätze ich mal, Du hast nicht genügend oft differenziert. Auch fürchte ich fast, daß Du da noch viel normieren mußt (alle Monate auf gleich lange Monate umrechnen) und daß Du ausgerechnet mit der schwierigsten Aufgabe angefangen hast, Multi-Saison, denn auch innerhalb der Woche gibt es Saison und auch innerhalb des Tages. Das kann man zwar wegnormieren, aber dafür braucht man ein gutes Meßverfahren, z.B. immer am 01. des Monats oder am ersten Sonntag des Monats um exakt Mitternacht ohne Zeitumstellungen, sprich immer Winter- oder Sommerzeit.

Aber gut ich guck’s mir mal an.

#9

Die „Saison innerhalb der Saison“ muss und kann vernachlässigt werden, da zum einen die Messdaten immer nur zum Monatsersten erhoben werden (das ist gegeben und nicht änderbar) und zum anderen soooooo exakt muss es nicht sein, daß da sogar Wochen-/Tages-/Wochenend-Schwankungen ermittelt werden. :slight_smile:

#10

Dumme Fragen dazu:

Der Backslash vor sqrt hat welche Bedeutung?
Was bedeuten die geschweiften Klammen um n (wieso keine runden Klammern)?
n ist meine Anzahl der Messwerte?
xm ist der Mittelwert meiner Messwerte? Oder gilt in dem Fall der Berechnete Wert (T+S) als die Stichprobe?
Was ist „Erwartungswert“ und was ist in dem Fall die Grundgesamtheit?
S wäre dann = SQRT(SUM((T-A)²)), wobei T der einzeln berechnete Wert (Trend+Saison) ist und A der Durchschnitt aller T’s?

Genau an diesen Fragen (was ist Erfahrungswert, was ist Grundgesamtheit, was ist die Stichprobe) scheiterte ich an sämtlichen Erklärungsversuchen im Internet - das meine ich mit „viel Vorwissen nötig“ :slight_smile:

P.S. Email ist raus an Dich!

#11

Sorry, das ist halbherzige TeX-Syntax.

Ja, n ist die Anzahl der Werte in S (identisch mit der Anzahl der Meßwerte in Deinem Fall). Xm das arithmetische Mittel der Saisonwerte. Der Erwartungswert der Saisonverteilung ist 0, denn anderenfalls hättest Du einen Trend in Deiner Saison und der hätte in die Trendkomponente gemußt.

Die Grundgesamtheit ist die wahre Verteilung der Saisonwerte, Deine ermittelten Werte sind ja nur Ziehungen daraus (eine Stichprobe).

S ist fast richtig, gibt’s da keine fertige Excel-Funktion für?

S = SQRT(SUM((S - Xm)^2)/(n-1))

Überall müssen bei Dir nur S-Werte rein, der Trend muß da komplett raus. Du mußt Dir im Klaren sein, was ein T-Test macht. Er besagt in etwa, daß Du Ziehungen mit Erwartungswert mu und Varianz sigma erwartest. Dann hast Du auf der anderen Seite eine Stichprobe (Deine S-Werte), diese hat einen (empirischen) Mittelwert (Xm). Wenn man das Ganze n-mal wiederholt, hast Du viele solcher Xm und die Größe (Xm - mu) ist t-verteilt mit Standardabweichung sigma / sqrt(n). Wenn Du jetzt Deine konkrete Stichprobe einsetzt, und stellst eine große Abweichung in der Größe (Xm - mu) fest (also größer oder kleiner als 0), dann kannst Du anhand der t-Verteilung (oder anderer angenommener Verteilungen) genau sagen, wie wahrscheinlich eine Messung ist, die noch größer oder kleiner ist, als der von Dir gemessene Wert. Das ist der sogenannte p-Wert. Wenn dieser klein ist, oder kleiner als eine vorgegebene Schranke, dann sagt man die Hypothese wurde als unwahrscheinlich abgelehnt bzw. der Meßwert hat eine hohe Signifikanz.

Nun ja, der Begriffsapparat ist wirklich erstmal eine kleine Hürde, aber er ist total wichtig, weil mit Grundbegriffen höhere Konzepte mit eigenen Begriffen eingeführt werden und darauf aufbauend wiederum höhere Konzepte usw.

Ich guck mir die Daten gleich an.

#12

Also, Auswertung gemacht. Gute und schlechte Nachrichten. Die Zerlegung hast Du in meinen Augen richtig gemacht (zumindest was lineare Regression angeht).

Schlechte Nachricht von der Signifikanzseite her: Die S-Komponente hat den One-Sample-Test nicht bestanden und auch den Welch-Test nicht. p-Wert ist 0.4996 und damit deutlich größer als z.B. 0.05.

Man hätte es auch schon ein wenig ahnen können, weil die Residuen ja in derselben Größenordnung liegen wie die Saison.

Aus Spaß hab ich auch mit STL mal einen Fit versucht:

stl

Wie eingangs erwähnt kommt der Trend aus einem ARIMA-Modell, ist also mächtiger als eine Regressionsgerade, aber auch hier liegen Residuen und Saison in der gleichen Größenordnung (p-Wert ist sogar noch schlechter als bei Dir: 0.5001)

#13

Mag sein, aber ich will es „zu Fuß“ bauen, damit ich es 100% verstehe und nachvollziehen kann. Excel ist für mich nur ein Zwischenschritt, das ganze baue ich dann letztlich in SQL nach, um es für viele Messwert-Reihen gleicher Art laufen zu lassen.

Das krieg ich hin :slight_smile:

OK, so langsam dämmert’s bei mir im Hirn :slight_smile:

Das hab ich gemerkt … ich glaube, um das wirklich vollends (auch für die Zukunft) zu verstehen, muss
ich noch viel lernen …

Ach, das ist keine schlechte Nachricht - es ist ein Ergebnis … schlecht wäre, wenn wir nicht zu einem Ergebnis kämen :slight_smile:

So, ich mache mich dann mal an die Umsetzung und schaue mal, ob ich auf die gleichen Werte komme wie Du.

#14

Hm, mir fällt da gerade etwas auf zum Thema T = sqrt(n) * (Xm - mu) / S …

  • wenn Xm das arithmetische Mittel der Saisonwerte ist und das Mittel der Saisonwerte 0 sein soll
  • mu auch 0 sein soll
  • dann ist der Term (xm-mu) doch ebenfalls immer 0 und somit wäre T auch immer 0

Jetzt bin ich echt verwirrt :smiley:

#15

Xm ist eine Stichprobe, die hat natürlich nicht exakt mean 0, sondern bei Dir -8.3e-4 und bei mir 7.5e-8. Außerdem ist (Xm - mu) ja immer so gebaut, daß da im Zähler 0 stehen soll, man will ja gerade beweisen, wie selten die Werte einer Stichprobe im Vergleich mit einem um den Erwartungswert mu t-verteilten Zufallsgenerator sind. Ein p-Wert von 0.05 heißt, dieser Stichprobenwert wird nur von 5% der Ziehungen aus dem Zufallsgenerator erreicht oder übertroffen.

#16

Ah, bessere Erklärung. Nimm als Xm nicht alle Deine Saisonwerte, sondern zufällig 6. Dann hast Du 6 Stichproben à 6 Werte. Jede Stichprobe hat einen Mean, diese 6 Means, so postulieren wir, sind t-verteilt um 0 (unser mu) mit Varianz S/sqrt(6) (S ist die empirische Standardabweichung der 6 means). Wenn man so an die Sache herangeht, erhält man andere p-Werte und auch eine andere Signifikanzaussage.

#17

Mal 'ne Zwischenfrage, ist das ein persönliches Projekt oder etwas ernsthafteres?

#18

Könnte ich so machen - und was stelle ich denn mit den 6 T-Werten an? Oder soll ich gleich für jeden einzelnen Saisonwert einen T-Wert berechnen? Dann habe ich 36 T-Werte :slight_smile:

#19

Andererseits fällt mir gerade auf: ich habe ja eh nur 12 (und nicht 36) Saisonwerte - die wiederholen sich ja exakt (da der Trend ja eben nicht mehr mit drin ist, sind es exakt die gleichen Werte).

#20

Hehe, nein nein, das war nur für Dich zur Erklärung, um zu verstehen, was ein t-test macht. Die üblichen Einführungen in die Statistik nehmen dafür Münzen, ich wollte es anhand Deiner Daten verdeutlichen.

Wenn Du nach der Praxisrelevanz fragst, wie gesagt, ich halte t-Statistik hier an dieser Stelle unangebracht, deswegen meine Frage, ob das eine private Übung ist oder Teil von etwas „Größerem“. Auch fände ich mal spannend zu wissen, wie genau Du den t-test in SQL einbauen willst Ich hab’s bislang noch nicht erwähnt, aber da kommt noch ein numerisches Problem auf Dich zu: Die Verteilungsfunktion der t-Verteilung. Die brauchst Du für die p-Werte, denn p = cdf_t(v, n-1) mit v der Wert der t-Statistik wie oben und n=12. Allerdings braucht man für diese CDF die unvollständige Betafunktion oder, alternativ, die log-Gamma-Funktion. Würde mich mal interessieren, ob Du da aus SQL heraus noch numerische oder Statistiksoftware benutzen willst.

Zum Thema Praxisrelevanz: Anstelle der direkten t-Statistik würde ich (im „echten“ Leben) eine ACF (Autokorrelationsanalyse) mit den Saisonwerten machen und deren Signifikanz benutzen. Hier ein Beispiel:

acf

Auf der x-Achse die Zeit in Monaten, auf der y-Achse die Autokorrelation, blau gestrichelt die Signifikanzschwelle. Man sieht, daß es die S-Komponente wiederum saisonbehaftet ist, es gibt noch signifikant die Halbjahressaison (6 Monate Versatz) und gerade eben signifikant die Quartalssaison (3 Monate Versatz und negativ korrelliert), d.h., wenn’s in einem Monat hochgeht, denn geht’s im Mittel 3 Monate später runter (relativ zu dem Startmonat), wenn’s in einem Monat hoch geht, dann geht’s 6 Monate später auch hoch. Und hoch und runter kann man noch vertauschen.

Aber, um es noch praktischer und rechnerisch einfacher zu machen, kannst Du auch die Standardabweichung der S-Komponente relativ zur Standardabweichung der Residuen angeben. Diese Idee kommt aus der Signalverarbeitung und gibt an, wie stark Dein Signal gegenüber Rauschen heraussticht. In Deinem Fall mit Deiner Zerlegung kommt hier: 2.3 heraus oder 7.2 dB (wie es der Signaltechniker sagen würde). Nur so als Idee.